Fluid dynamics is the study of fluids in motion and corresponding phenomena. A fluid in motion has a velocity, just as a solid object in motion has a velocity. Like the velocity of a solid, the velocity of a fluid is the rate of change of position per unit of time. In mathematical terms, the velocity of a fluid is the derivative of the position vector of the fluid with respect to time, and is therefore itself a vector quantity. The flow velocity vector is a function of position, and if the velocity of the fluid is not constant then it is also a function of time. Equation 1 shows the mathematical expression for the velocity of a fluid in motion. As a vector quantity, fluid velocity must have at least one non-zero directional component and may have up to three non-zero directional components. The velocity vector has non-zero components in any orthogonal direction along which motion of the fluid occurs.
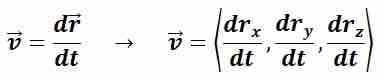
Flow Velocity
Mathematical Expression for Flow Velocity
Turbulent Flow vs. Laminar Flow
Fluid velocity can be affected by the pressure of the fluid, the viscosity of the fluid, and the cross-sectional area of the container in which the fluid is travelling. These factors affect fluid velocity depending on the nature of the fluid flow—particularly whether the flow is turbulent or laminar in nature. In the case of turbulent flow, the flow velocity is complex in nature and thus hard to predict; it must be analyzed on a system per system basis. In the case of Laminar flow, however, fluid flow is much simpler and flow velocity can be accurately calculated using Poiseuille's Law. In SI units, fluid flow velocity is expressed in terms of meters per seconds. The magnitude of the fluid flow velocity is the fluid flow speed. Fluid flow velocity effectively describes everything about the motion of a fluid.
Volumetric Flow
In addition to flow velocity, volumetric flow rate is an important quantity in fluid dynamics analysis. Volumetric flow is defined as the volume of fluid that passes through a given surface per unit time. Qualitatively, Figure 1 shows the notion of volumetric flow rate regarding a cross-sectional surface of area A. Mathematically, volumetric flow rate is the derivative of the volume of fluid that passes through a given surface with respect to time; in SI units this is expressed as meterscubed per second. Volumetric flow rate is related to the flow velocity vector as the surface integral with respect to the surface in question. If the surface area in question is a flat, plane cross-section, the surface integral reduces as shown in Equation 2 , where A is the surface area of the surface in question and v is the flow velocity of the fluid.
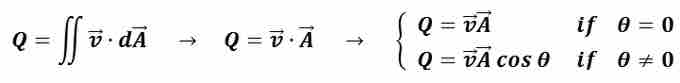
Volumetric Flow Rate
Volumetric Flow Rate Surface Integral and its simplification
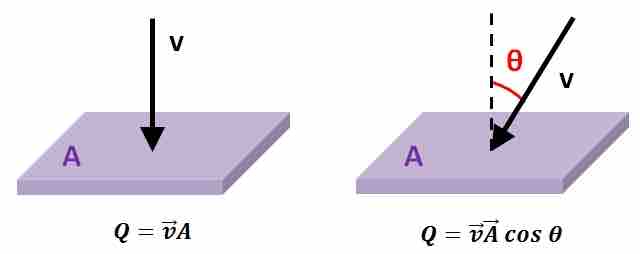
Flow Velocity - Volumetric Flow Rate Relation
This figure shows the relation between flow velocity and volumetric flow rate.
Moreover, only the flow velocity component parallel to the surface normal of the surface in question, or alternatively the flow velocity component perpendicular to the surface in question contributes to the volumetric flow rate. Figure 1 and Equation 2 illustrate decomposition of the flow velocity vector, making an angle θ with respect to the normal of the surface plane in order to calculate volumetric flow rate through that surface. Thus, volumetric flow rate for a given fluid velocity and cross-sectional surface area increases as θ decreases, and is maximized when θ = 0. Volumetric flow rate is an important scalar quantity in fluid dynamics and is used widely in fluid flow measurements. Volumetric flow rate can be converted to mass flow rate if the density of the fluid is known. Flow of fluids through a closed system is often analyzed as a hydraulic circuit analogous to electron flow in an electronic circuit where: 1) the volumetric fluid flow is analogous to the electric current, 2) pressure is analogous to the voltage, and 3) fluid velocity is analogous to current density.