Torricelli's law is theorem in fluid dynamics about the relation between the exit velocity of a fluid from a sharp-edged hole in a reservoir to the height of the fluid above that exit hole . This relationship applies for an "ideal" fluid (inviscid and incompressible) and results from an exchange of potential energy,
This relationship can be derived by applying the Bernoulli equation between the top of the reservoir and the exit hole . Applying Bernoulli between the top of a reservoir and an exit hole at a height h below the top of the reservoir results in,

Exchange of Energy
Potential energy at the top of the reservoir becomes kinetic energy at the exit.
where subscript t implies evaluation at the top of the reservoir and subscript e implies evaluation at the exit. If we assume both the top of reservoir and the exit are open to the atmosphere, the zero for potential energy is at the exit hole, and the fluid velocity at the top of the reservoir is essentially zero (large reservoir, small hole), we arrive at
This can be solved for the exit velocity, resulting in,
where again ht is the height difference between the top of the reservoir and the exit hole. Due to the assumption of an ideal fluid, all forces acting on the fluid are conservative and thus there is an exchange between potential and kinetic energy. The result is that the velocity acquired by the fluid is the same that a body would acquire when simply dropped from the height ht.
A simple experiment to test Torricelli's law involves filling a soda bottle with water and puncturing the bottom with a small hole (about 1 cm in diameter). As the height in the reservoir decreases, the exit velocity will decrease as well. The exit velocity can be increased by capping the top of the reservoir and pressurizing it .
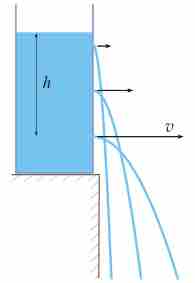
Toricelli's Law
The exit velocity depends on the height of the fluid above the exit hole.
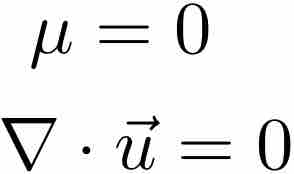
Ideal Fluid
Applies to an ideal fluid (inviscid, incompressible)