Maxwell's Equations

Maxwell's Equations

Maxwell's equations are a set of four partial differential equations that, along with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits.

Named after esteemed physicist James Clerk Maxwell, the equations describe the creation and propagation of electric and magnetic fields. Fundamentally, they describe how electric charges and currents create electric and magnetic fields, and how they affect each other.

Maxwell's equations can be divided into two major subsets. The first two, Gauss's law and Gauss's law for magnetism, describe how fields emanate from charges and magnets respectively. The other two, Faraday's law and Ampere's law with Maxwell's correction, describe how induced electric and magnetic fields circulate around their respective sources.

Each of Maxwell's equations can be looked at from the "microscopic" perspective, which deals with total charge and total current, and the "macroscopic" set, which defines two new auxiliary fields that allow one to perform calculations without knowing microscopic data like atomic-level charges.

Gauss's Law

Gauss's law relates an electric field to the charge(s) that create(s) it. The field (E) points towards negative charges and away from positive charges, and from the microscopic perspective, is related to charge density (ρ) and vaccuum permittivity (ε₀, or permittivity of free space) as:

$\nabla \cdot \bf E=\frac {\rho}{\epsilon_0}$

Gauss's Law basically says that a net amount of charge contained within a region of space will generate an electric field that emanates through the surface that surrounds that region.

Example of Gauss's Law

A positive charge contained within a region of space creates an electric field that emanates from the surface of that region.

Gauss's Law for Magnetism

Gauss's law for magnetism states that there are no "magnetic charges (or monopoles)" analogous to electric charges, and that magnetic fields are instead generated by magnetic dipoles. Such dipoles can be represented as loops of current, but in many ways are similar in appearance to positive and negative "magnetic charges" that are inseparable and thus have no formal net "magnetic charge."

Magnetic field lines form loops such that all field lines that go into an object leave it at some point. Thus, the total magnetic flux through a surface surrounding a magnetic dipole is always zero.

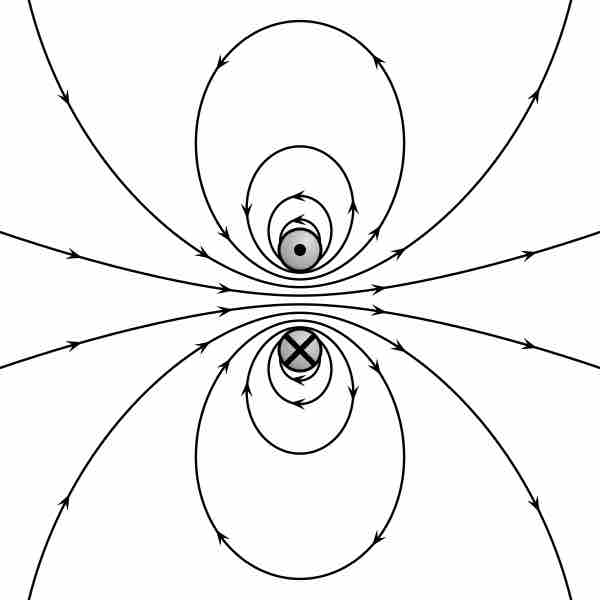
Field lines caused by a magnetic dipole

The field lines created by this magnetic dipole either form loops or extend infinitely.

The differential form of Gauss's law for magnetic for magnetism is

$\nabla \cdot \bf B= 0$

Faraday's Law

Faraday's law describes how a time-varying magnetic field (or flux) induces an electric field. The principle behind this phenomenon is used in many electric generators. Both macroscopic and microscopic differential equations are the same, relating electric field (E) to the time-partial derivative of magnetic field (B):

$\nabla \times \bf E=-\frac {\partial \bf B}{\partial t}$

Ampere's Circuital Law (with Maxwell's correction)

Ampere's law originally stated that magnetic field could be created by electrical current. Maxwell added a second source of magnetic fields in his correction: a changing electric field (or flux), which would induce a magnetic field even in the absence of an electrical current. He named the changing electric field "displacement current."

Maxwell's correction shows that self-sustaining electromagnetic waves (light) can travel through empty space even in the absence of moving charges or currents, with the electric field component and magnetic field component each continually changing and each perpetuating the other.

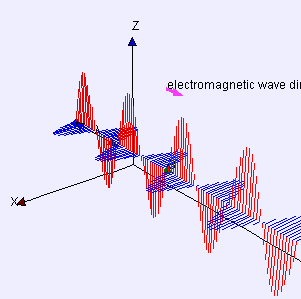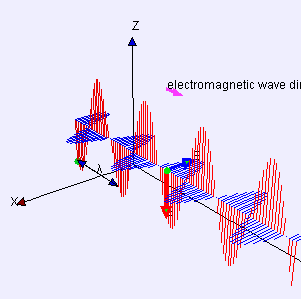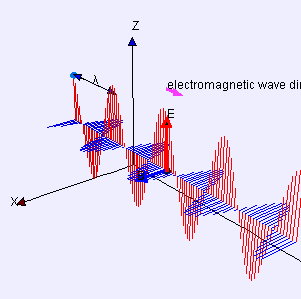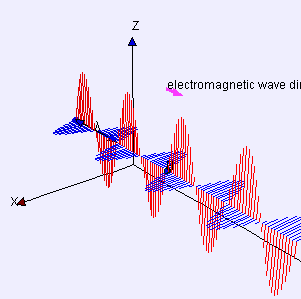
Electromagnetic Waves

Electric (red) and magnetic (blue) waves propagate in phase sinusoidally, and perpendicularly to one another.

The microscopic approach to the Maxwell-corrected Ampere's law relates magnetic field (B) to current density (J, or current per unit cross sectional area) and the time-partial derivative of electric field (E):

$\nabla \times \bf B=\mu_0 \bf J + \mu_0 \epsilon_0 \frac {\partial \bf E}{\partial t}$