Superposition of Electric Potential

To find the total electric potential due to a system of point charges, one adds the individual voltages as numbers.

Learning Objective

Explain how the total electric potential due to a system of point charges is found

Key Points

The electric potential V is a scalar and has no direction, whereas the electric field E is a vector.
To find the voltage due to a combination of point charges, you add the individual voltages as numbers. So for example, in the electric potential at point L is the sum of the potential contributions from charges Q₁, Q₂, Q₃, Q₄, and Q₅ so that $V_{L}=k[\frac{Q_{1}}{d_{1}}+\frac{Q_{2}}{d_{2}}+\frac{Q_{3}}{d_{3}}+\frac{Q_{4}}{d_{4}}+\frac{Q_{5}}{d_{5}}]$.
To find the total electric field, you must add the individual fields as vectors, taking magnitude and direction into account. This is consistent with the fact that V is closely associated with energy, a scalar, whereas E is closely associated with force, a vector.
The summing of all voltage contributions to find the total potential field is called the superposition of electric potential. It is much easier to sum scalars than vectors, so often the preferred method for solving problems with electric fields involves the summing of voltages.

Terms

scalar
A quantity that has magnitude but not direction; compare vector.
vector
A directed quantity, one with both magnitude and direction; the between two points.
superposition
The summing of two or more field contributions occupying the same space.

Full Text

Superposition of Electric Potential

We've seen that the electric potential is defined as the amount of potential energy per unit charge a test particle has at a given location in an electric field, i.e.

$V=\frac{PE}{q}$

We've also seen that the electric potential due to a point charge is

where k is a constant equal to 9.0×10⁹ N⋅m²/C². The equation for the electric potential of a point charge looks similar to the equation for the electric field generated for a point particle

$E=\frac{F}{q}=\frac{kQ}{r^{2}}$

with the difference that the electric field drops off with the square of the distance while the potential drops off linearly with distance. This is analogous to the relationship between the gravitational field and the gravitational potential .

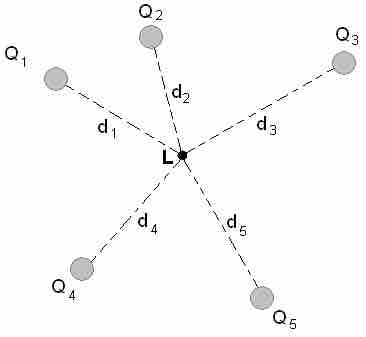
Superposition of Electric Potential

The electric potential at point L is the sum of voltages from each point charge (scalars).

Recall that the electric potential V is a scalar and has no direction, whereas the electric field E is a vector. To find the voltage due to a combination of point charges, you add the individual voltages as numbers. So for example, in the figure above the electric potential at point L is the sum of the potential contributions from charges Q₁, Q₂, Q₃, Q₄, and Q₅ so that

$V_{L}=k[\frac{Q_{1}}{d_{1}}+\frac{Q_{2}}{d_{2}}+\frac{Q_{3}}{d_{3}}+\frac{Q_{4}}{d_{4}}+\frac{Q_{5}}{d_{5}}]$

To find the total electric field, you must add the individual fields as vectors, taking magnitude and direction into account. This is consistent with the fact that V is closely associated with energy, a scalar, whereas E is closely associated with force, a vector.

The summing of all voltage contributions to find the total potential field is called the superposition of electric potential. Summing voltages rather than summing the electric simplifies calculations significantly, since addition of potential scalar fields is much easier than addition of the electric vector fields. Note that there are cases where you might need to sum potential contributions from sources other than point charges; however, that is beyond the scope of this section.

[ edit ]

Prev Concept

Electric Potential Due to a Point Charge

Capacitance

Next Concept