Energy is conserved in the movement of a charged particle through an electric field, as it is in every other physical situation. This phenomenon can be expressed as the equality of summed kinetic (Ekin) and electric potential (Eel) energies:
Given a stationary test charge in a certain location, an applied electric field will cause the charge to move to one end or the other, depending on the charge (positive test charges will move in the direction of the field; negative charges will move in the opposite direction). In all cases, a charge will naturally move from an area of higher potential energy to an area of lower potential energy.
At the instant at which the field is applied, the motionless test charge has 0 kinetic energy, and its electric potential energy is at a maximum. After that moment, the charge accelerates, and its kinetic energy (from motion) increases as its potential energy decreases. Throughout this time, the sum of potential and kinetic energies remains constant.
Another way to express the previous equation is:
where m and v are the mass and velocity of the electron, respectively, and U is the electric potential energy. U can be calculated as follows:
where V is the potential difference, k is a constant, q0 is a test charge, q is another charge, and r is the distance between the charges.
The terms involved in the formula for conservation of energy can be rewritten in many ways, but all expressions are based on the simple premise of equating the initial and final sums of kinetic and potential energy.
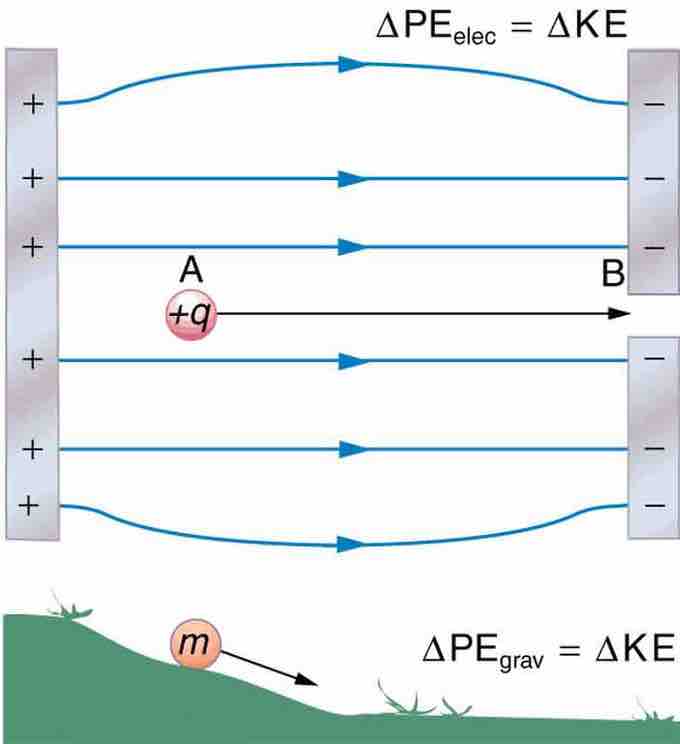
Similarities Between Activity of Gravitational and Electric Fields on an Object
The charge, +q, is moved down the electric field in the same way that the object, m, is moved down the hill. In both instances, the particle in motion goes from a higher to a lower potential energy state.