Resistors and Capacitors in Series

An RC circuit is one containing a resistor R and a capacitor C. The capacitor is an electrical component that houses electric charge. In this Atom, we will study how a series RC circuit behaves when connected to a DC voltage source. (In subsequent Atoms, we will study its AC behavior. )

Charging

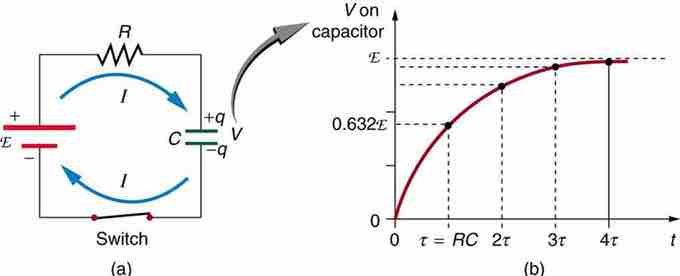
Fig 1 shows a simple RC circuit that employs a DC voltage source. The capacitor is initially uncharged. As soon as the switch is closed, current flows to and from the initially uncharged capacitor. As charge increases on the capacitor plates, there is increasing opposition to the flow of charge by the repulsion of like charges on each plate.

Charging an RC Circuit

(a) An RC circuit with an initially uncharged capacitor. Current flows in the direction shown as soon as the switch is closed. Mutual repulsion of like charges in the capacitor progressively slows the flow as the capacitor is charged, stopping the current when the capacitor is fully charged and Q=C⋅emf. (b) A graph of voltage across the capacitor versus time, with the switch closing at time t=0. (Note that in the two parts of the figure, the capital script E stands for emf, q stands for the charge stored on the capacitor, and τ is the RC time constant. )

In terms of voltage, across the capacitor voltage is given by V_c=Q/C, where Q is the amount of charge stored on each plate and C is the capacitance. This voltage opposes the battery, growing from zero to the maximum emf when fully charged. Thus, the current decreases from its initial value of I₀=emf/R to zero as the voltage on the capacitor reaches the same value as the emf. When there is no current, there is no IR drop, so the voltage on the capacitor must then equal the emf of the voltage source.

Initially, voltage on the capacitor is zero and rises rapidly at first since the initial current is a maximum. Fig 1 (b) shows a graph of capacitor voltage versus time (t) starting when the switch is closed at t=0. The voltage approaches emf asymptotically since the closer it gets to emf the less current flows. The equation for voltage versus time when charging a capacitor C through a resistor R, is:

$V(t)= emf(1-e^{t/RC})$,

where V(t) is the voltage across the capacitor and emf is equal to the emf of the DC voltage source. (The exact form can be derived by solving a linear differential equation describing the RC circuit, but this is slightly beyond the scope of this Atom. ) Note that the unit of RC is second. We define the time constant τ for an RC circuit as $\tau = RC$. τ shows how quickly the circuit charges or discharges.

Discharging

Discharging a capacitor through a resistor proceeds in a similar fashion, as illustrates. Initially, the current is I₀=V₀/R, driven by the initial voltage V₀ on the capacitor. As the voltage decreases, the current and hence the rate of discharge decreases, implying another exponential formula for V. Using calculus, the voltage V on a capacitor C being discharged through a resistor R is found to be

$V(t) = V_0 e^{-t/RC}$.