Introduction to Kirchhoff's Laws
Kirchhoff's circuit laws are two equations first published by Gustav Kirchhoff in 1845. Fundamentally, they address conservation of energy and charge in the context of electrical circuits.
Although Kirchhoff's Laws can be derived from the equations of James Clerk Maxwell, Maxwell did not publish his set of differential equations (which form the foundation of classical electrodynamics, optics, and electric circuits) until 1861 and 1862. Kirchhoff, rather, used Georg Ohm's work as a foundation for Kirchhoff's current law (KCL) and Kirchhoff's voltage law (KVL).
Kirchhoff's laws are extremely important to the analysis of closed circuits. Consider, for example, the circuit illustrated in the figure below, consisting of five resistors in a combination of in series and parallel arrangements. Simplification of this circuit to a combination of series and parallel connections is impossible. However, using Kirchhoff's rules, one can analyze the circuit to determine the parameters of this circuit using the values of the resistors (R1, R2, R3, r1 and r2). Also of importance in this example is that the values E1 and E2 represent sources of voltage (e.g., batteries).
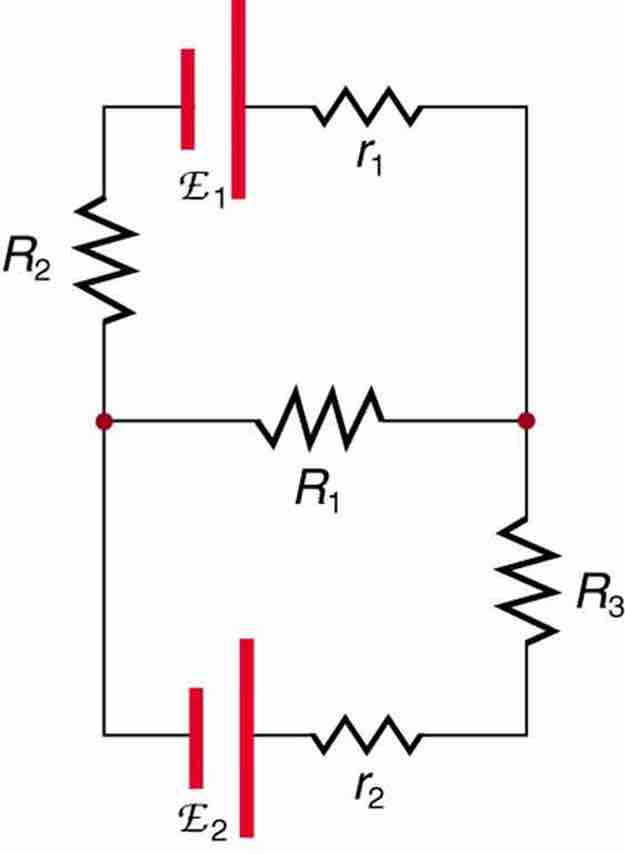
Closed Circuit
To determine all variables (i.e., current and voltage drops across the different resistors) in this circuit, Kirchhoff's rules must be applied.
As a final note, Kirchhoff's laws depend on certain conditions. The voltage law is a simplification of Faraday's law of induction, and is based on the assumption that there is no fluctuating magnetic field within the closed loop. Thus, although this law can be applied to circuits containing resistors and capacitors (as well as other circuit elements), it can only be used as an approximation to the behavior of the circuit when a changing current and therefore magnetic field are involved.