Applications

Overview

Kirchhoff's rules can be used to analyze any circuit by modifying them for those circuits with electromotive forces, resistors, capacitors and more. Practically speaking, however, the rules are only useful for characterizing those circuits that cannot be simplified by combining elements in series and parallel.

Combinations in series and parallel are typically much easier to perform than applying either of Kirchhoff's rules, but Kirchhoff's rules are more broadly applicable and should be used to solve problems involving complex circuits that cannot be simplified by combining circuit elements in series or parallel.

Example of Kirchoff's Rules

shows a very complex circuit, but Kirchhoff's loop and junction rules can be applied. To solve the circuit for currents I₁, I₂, and I₃, both rules are necessary.

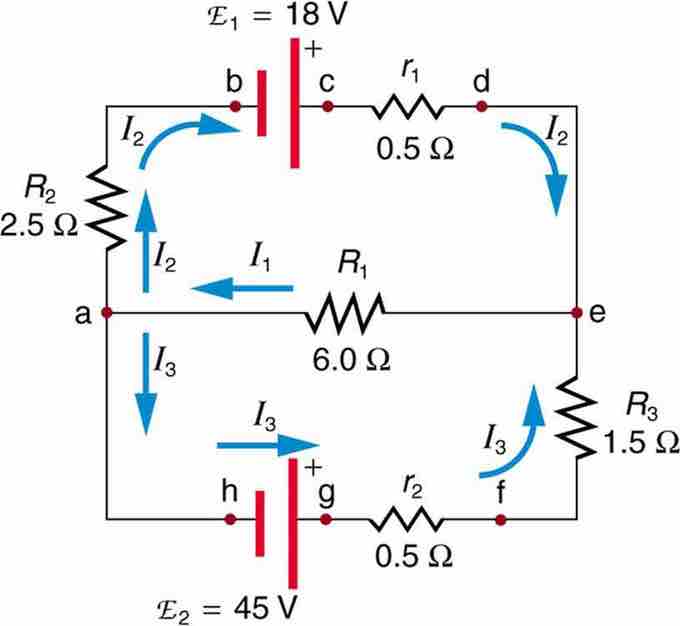
Kirchhoff's Rules: sample problem

This image shows a very complicated circuit, which can be reduced and solved using Kirchoff's Rules.

Applying Kirchhoff's junction rule at point a, we find:

$I_1=I_2+I_3$

because I₁ flows into point a, while I₂ and I3 flow out. The same can be found at point e. We now must solve this equation for each of the three unknown variables, which will require three different equations.

Considering loop abcdea, we can use Kirchhoff's loop rule:

$-I_2R_2+ \mathrm{emf}_1-I_2r_1-I_1R_1=-I_2(R_2)+r_1)+\mathrm{emf}_1-I_1R_1=0$

Substituting values of resistance and emf from the figure diagram and canceling the ampere unit gives:

$-3I_2+18-6I_1=0$

This is the second part of a system of three equations that we can use to find all three current values. The last can be found by applying the loop rule to loop aefgha, which gives:

$I_1R_1+I_3R_3+I_3r_2-\mathrm{emf}_2=I_1R_1+I_3(R_3+r_2)-\mathrm{emf}_2=0$

Using substitution and simplifying, this becomes:

$6I_1+2I_3-45=0$

In this case, the signs were reversed compared with the other loop, because elements are traversed in the opposite direction.

We now have three equations that can be used in a system. The second will be used to define I₂, and can be rearranged to:

$I_2=6-2I_1$

The third equation can be used to define I₃, and can be rearranged to:

$I_3=22.5-3I_1$

Substituting the new definitions of I₂ and I₃ (which are both in common terms of I₁), into the first equation (I₁=I₂+I₃), we get:

$I_1=(6-2I_1)+(22.5-3I_1)=28.5-5I_1$

Simplifying, we find that I₁=4.75 A. Inserting this value into the other two equations, we find that I₂=-3.50 A and I₃=8.25 A.