Bohr's condition, that the angular momentum is an integer multiple of
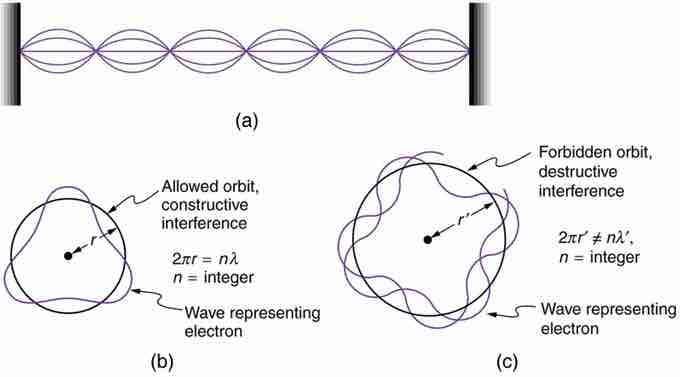
Waves on a String
(a) Waves on a string have a wavelength related to the length of the string, allowing them to interfere constructively. (b) If we imagine the string bent into a closed circle, we get a rough idea of how electrons in circular orbits can interfere constructively. (c) If the wavelength does not fit into the circumference, the electron interferes destructively; it cannot exist in such an orbit.
Allowed orbits are those in which an electron constructively interferes with itself. Not all orbits produce constructive interference and thus only certain orbits are allowed (i.e., the orbits are quantized). By assuming that the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron's orbit, we have the equation:
Substituting de Broglie's wavelength of
Rearranging terms, and noting that
As previously stated, Bohr was forced to hypothesize this rule for allowed orbits. We now realize this as the condition for constructive interference of an electron in a circular orbit.
Accordingly, a new kind of mechanics, quantum mechanics, was proposed in 1925. Bohr's model of electrons traveling in quantized orbits was extended into a more accurate model of electron motion. The new theory was proposed by Werner Heisenberg. By different reasoning, another form of the same theory, wave mechanics, was discovered independently by Austrian physicist Erwin Schrödinger. Schrödinger employed de Broglie's matter waves, but instead sought wave solutions of a three-dimensional wave equation. This described electrons that were constrained to move about the nucleus of a hydrogen-like atom by being trapped by the potential of the positive nuclear charge.