To consider why wave nature of matter in bound systems leads to quantization, let's consider an example in classical mechanics. We will look at a basic string "instrument" (a string pulled tight and fixed at both ends). If a string was free and not attached to anything, we know that it could oscillate at any driven frequency. However, the string in this example (with fixed ends and specific length) can only produce a very specific set of pitches because only waves of a certain wavelength can "fit" on the string of a given length with fixed ends. Once the string becomes a "bound system" with specific boundary restrictions, it allows waves with only a discrete set of frequencies.
This is the exact mechanism that causes quantization in atoms. The wave nature of matter is responsible for the quantization of energy levels in bound systems. Just like a free string, the matter wave of a free electron can have any wavelength, determined by its momentum. However, once an electron is "bound" by a Coulomb potential of a nucleus, it can no longer have an arbitrary wavelength as the wave needs to satisfy a certain boundary condition. Only those states where matter interferes constructively (leading to standing waves) exist, or are "allowed" (see illustration in.
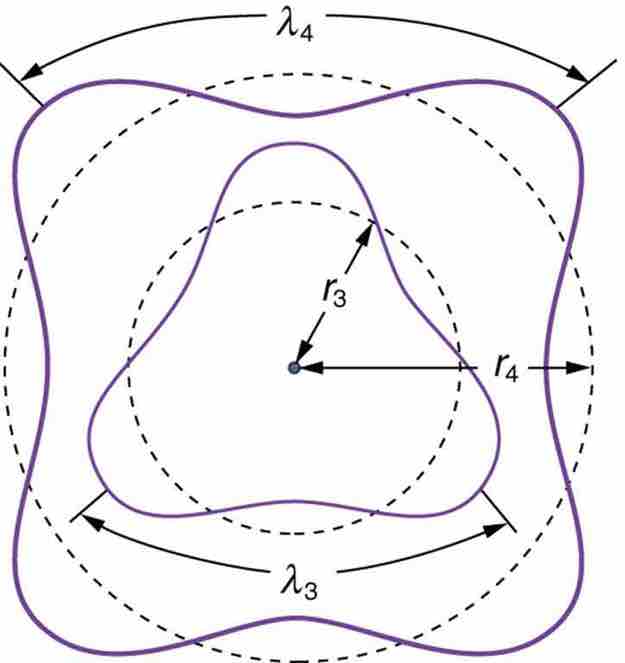
Fig 2
The third and fourth allowed circular orbits have three and four wavelengths, respectively, in their circumferences.
Assuming that an integral multiple of the electron's wavelength equals the circumference of the orbit, we have:
Substituting
The angular momentum is
As previously discussed, Bohr was forced to hypothesize this as the rule for allowed orbits. We now realize this as a condition for constructive interference of an electron in a (bound) circular orbit.