Marginal Analysis
Pricing decisions tend to heavily involve analysis regarding marginal contributions to revenues and costs. Specifically, firms tend to accomplish their objective of profit maximization by increasing their production until marginal revenue equals marginal cost, and then charging a price which is determined by the demand curve.
In business, the practice of setting the price of a product to equal the extra cost of producing an extra unit of output is known as marginal-cost pricing. Businesses often set prices close to marginal cost during periods of poor sales. If, for example, an item has a marginal cost of $1.00 and a normal selling price of $2.00 the firm selling the item might wish to lower the price to $1.10 if demand has waned. The business would choose this approach because the incremental profit of 10 cents from the transaction is better than no sale at all.
In the marginal analysis of pricing decisions, if marginal revenue is greater than marginal cost at some level of output, marginal profit is positive and thus a greater quantity should be produced. Alternatively, if marginal revenue is less than the marginal cost, marginal profit is negative and a lesser quantity should be produced. At the output level at which marginal revenue equals marginal cost, marginal profit is zero and this quantity is the one that maximizes profit.
Since total profit increases when marginal profit is positive and total profit decreases when marginal profit is negative, it must reach a maximum where marginal profit is zero.
In , the intersection of MR and MC is shown as point A. If the industry is perfectly competitive (as is assumed in the diagram), the firm faces a demand curve (D) that is identical to its marginal revenue curve (MR). Thus, this is a horizontal line at a price determined by industry supply and demand. If the firm is operating in a non-competitive market, changes would have to be made to the diagram.
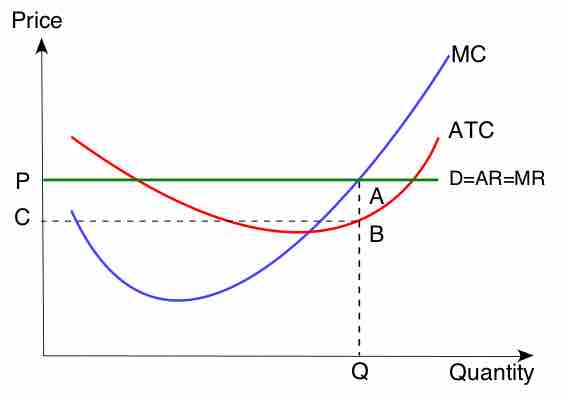
Marginal Profit Maximization
This series of cost curves shows the implementation of profit maximization using marginal analysis.
For example, the marginal revenue curve would have a negative gradient, due to the overall market demand curve. In a non-competitive environment, more complicated profit maximization solutions involve the use of game theory. In some cases, a firm's demand and cost conditions are such that marginal profits are greater than zero for all levels of production up to a certain maximum. In this case, marginal profit plunges to zero immediately after that maximum is reached. Thus, output should be produced at the maximum level, which also happens to be the level that maximizes revenue. In other words, the profit maximizing quantity and price can be determined by setting marginal revenue equal to zero, which occurs at the maximal level of output.