Calculating the Yield of an Annuity

The yield of an annuity is commonly found using either the percent change in the value from PV to FV, or the internal rate of return.

Learning Objective

Calculate the yield of an annuity using the internal rate of return method

Key Points

The yield of an annuity may be found by discounting to find the PV, and then finding the percentage change from the PV to the FV.
The Internal Rate of Return (IRR) is the discount rate at which the NPV of an investment equals 0.
The IRR calculates an annualized yield of an annuity.

Terms

Net Present Value (NPV)
The present value of a project or an investment decision determined by summing the discounted incoming and outgoing future cash flows resulting from the decision.
Internal Rate of Return (IRR)
The discount rate that will cause the NPV of an investment to equal 0.
yield
In finance, the term yield describes the amount in cash that returns to the owners of a security. Normally it does not include the price variations, at the difference of the total return. Yield applies to various stated rates of return on stocks (common and preferred, and convertible), fixed income instruments (bonds, notes, bills, strips, zero coupon), and some other investment type insurance products

Full Text

The yield of annuity can be calculated in similar ways to the yield for a single payment, but two methods are most common.

The first is the standard percentage-change method. Just as for a single payment, this method calculated the percentage difference between the FV and the PV. Since annuities include multiple payments over the lifetime of the investment, the PV (or V₁ in is the present value of the entire investment, not just the first payment.

The second popular method is called the internal rate of return (IRR). The IRR is the interest rate (or discount rate) that causes the Net Present Value (NPV) of the annuity to equal 0. That means that the PV of the cash outflows equals the PV of the cash inflows. The higher the IRR, the more desirable is the investment. In theory, you should make investment with an IRR greater than the cost of capital.

Let's take an example investment: It is not technically an annuity because the payments vary, but still is a good example for how to find IRR:

Suppose you have a potential investment that would require you to make a $4,000 investment today, but would return cash flows of $1,200, $1,410, $1,875, and $1,050 in the four successive years. This investment has an implicit rate of return, but you don't know what it is. You plug the numbers into the NPV formula and set NPV equal to 0. You then solve for r, which is your IRR (it's not easy to solve this problem by hand. You will likely need to use a business calculator or Excel). When r = 14.3%, NPV = 0, so therefore the IRR of the investment is 14.3%.

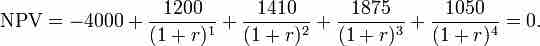
IRR Example

The setup to find the IRR of the investment with cash flows of -4000, 1200, 1410, 1875, and 1050. By setting NPV = 0 and solving for r, you can find the IRR of this investment.

[ edit ]

Prev Concept

Calculating the Yield of a Single-Period Investment

Understanding the Cost of Money

Next Concept