One of the most fundamental concepts in finance is the Time Value of Money. It states that money today is worth more than money in the future.
Imagine you are lucky enough to have someone come up to you and say "I want to give you $500. You can either have $500 right now, or I can give you $500 in a year. What would you prefer? " Presumably, you would ask to have the $500 right now. If you took the money now, you could use it to buy a TV. If you chose to take the money in one year, you could still use it to buy the same TV, but there is a cost. The TV might not be for sale, inflation may mean that the TV now costs $600, or simply, you would have to wait a year to do so and should be paid for having to wait. Since there's no cost to taking the money now, you might as well take it.
There is some value, however, that you could be paid in one year that would be worth the same to you as $500 today. Say it's $550- you are completely indifferent between taking $500 today and $550 next year because even if you had to wait a year to get your money, you think $50 is worth waiting.
In finance, there are special names for each of these numbers to help ensure that everyone is talking about the same thing. The $500 you get today is called the Present Value (PV). This is what the money is worth right now. The $550 is called the Future Value (FV). This is what $500 today is worth after the time period (t)- one year in this example. In this example money with a PV of $500 has a FV of $550. The rate that you must be paid per year in order to not have the money is called an Interest Rate (i or r).
All four of the variables (PV, FV, r, and t) are tied together in the equation in . Don't worry if this seems confusing; the concept will be explored in more depth later.
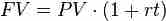
Simple Interest Formula
Simple interest is when interest is only paid on the amount you originally invested (the principal). You don't earn interest on interest you previously earned.