Productivity, in economic terms, measures inputs and outputs to derive overall production efficiency within a system. Simply put, it measures how much can you get out of what you put into a given system. Increased productivity means more output is produced from the same amount of inputs. In order to generate meaningful information about the productivity of a given system, production functions are used to measure it. Understanding the way in which productivity metrics function, one can more comprehensively grasp the concept and employ it in a meaningful way.
Production Function
From an economic standpoint, the production function demonstrates the tangible output created as a result of a production process including all tangible inputs. The objective in employing this perspective is to pursue allocative efficiency within the process (as opposed to technical or logistical efficiency, as engineers or supply chain managers may be pursuing). This means that the production function identifies optimal inputs (and consequent outputs) to satisfy the needs of a given population via a particular production process. While different economic perspectives often identify different factors of production (i.e. inputs in the system), it is useful to identify the following:
- Land/Natural Resources:Products of nature that have economic value, including metals/agriculture/livestock/land/etc.
- Capital: This is a broad term, capturing more than just financing and investment. Capital can also be fixed capital (i.e. machinery, equipment, buildings, computers, etc.) or working capital (i.e. goods, inventory and liquid assets). Concepts of human, intellectual and social capital is also highlighted, separate from the concept of labor below, which can affect the efficiency of a process.
- Labor: The human skills, time and efforts necessary to add value to the production process. This can range from highly tangible inputs (working hours, products assembled) to highly intangible inputs (entrepreneurship, experience, technology skills, etc.).
Conceptually, the production function makes certain assumptions of the maximum potential production, availability of inputs and demand for outputs to create a boundary of potential production. This will include the derivation of a marginal product for each factor (see ), or essentially the extra output that can be created for each additional unit of input. Naturally, this is theoretically subjected to the concept of diminishing marginal returns, where the marginal product of a given input (in the figure we are illustrating labor) will fall as the starting points for quantity rise.
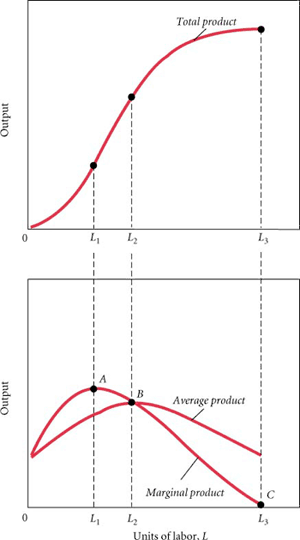
Product Function
This graph illustrates the way in which a production function identifies the relationship between a quantity of inputs and the resulting output of a given product. This takes into account marginal and average product, which are indicative of the change in efficiency based upon inputs.
Forms of the Production Function
There are a variety of ways to approach the measuring of productivity in the context of production functions:
- Functional Form: One way a production function can be illustrated is through the following equation
$Q = f(X_1,X_2,X_3,...,X_n)$ . In this circumstance 'Q' is the quantity of output while each 'x' is a factor input. - Linear Form: While this is generally not practical in practice, it is also possible to represent this in a linear mathematical fashion if parameters (a, b, c, and d below) are identified:
$Q=a+b X_1+c X_2+d X_3+ ...$ - Cobb-Douglas Production Function: One of the most useful frameworks, that allow for a technological relationship to be illustrated between the amount of two (or more) inputs is the Cobb-Douglas model. This is most often used to illustrate how physical capital and labor effect one another (see ). In the equation, 'Y' is total production while 'L' is labor, 'K' is capital, 'A' is total factor productivity and the alpha and beta are the elasticity of the two inputs.
$Y=AL^{\beta}K^{\alpha}$ - Leontief Production Function: The Leontief Production Function assumes a technologically pre-determined set of proportions for the factors of production (i.e. no ability to substitute between factors. This is specifically designed to capture minimums or limiting cases of production. The 'z's in the equation are inputs of specific goods while the a and b represent the technological determined constants and 'q' being the overall output:
$q = \text{Min}\left(\frac{z_1}{a},\frac{z_2}{b}\right)$
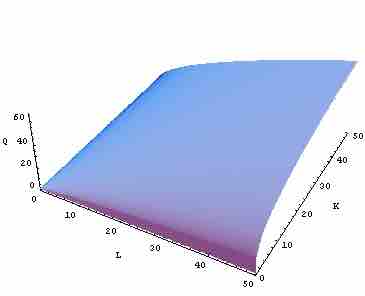
Cobb-Douglas Production Function
This is an illustration of a two-input Cobb-Douglas Production Function, where the ability to benchmark an output in comparison to two separate quantities of inputs is feasible.