Surface Tension

Liquids are Fluids

Liquids and solids share a common attribute: a clear and discernible phase boundary that gives the sample a simple but definite shape. Liquids and solids share also something else: most of their molecular units are to some extent in relatively close contact. However, liquids, like gases, are fluids, meaning that their molecular units can move more or less independently of each other. Whereas the volume of a gas depends entirely on the pressure, the volume of a liquid is largely independent of the atmospheric pressure. Therefore, gases are compressible while liquids are very nearly not.

Cohesive Forces Result in Surface Tension

The molecules in a sample of a liquid that find themselves fully in the interior volume are surrounded by other molecules and interact with them based on the attractive intermolecular forces that are present for molecules of this type. However, the molecules at the interface with another medium (usually air) do not have other like molecules on all of their sides (namely, on top of them), so they cohere more strongly to the molecules on the surface and immediately below them. The result is a surface film which makes it more difficult for an object to pierce through the surface than for it to move once submerged in the sample of liquid. Therefore, the cohesive forces result in the phenomenon of surface tension.

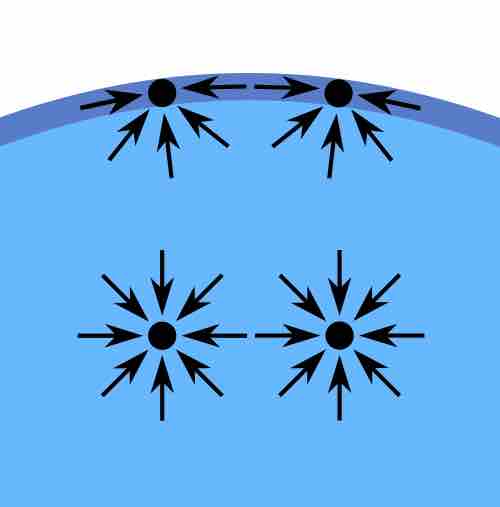
Diagram of forces on molecules in a liquid

In the bulk of the liquid, the forces are the same in all directions, while at the surface, the net effect is "downward," into the interior.

The Young-Laplace Equation

Surface tension is responsible for the shape of a liquid droplet. Although easily deformed, droplets of water tend to be pulled into a spherical shape by the cohesive forces of the surface layer. In the absence of other forces, including gravity, drops of virtually all liquids would be perfectly spherical. If no force acts normal (perpendicular) to a tensioned surface, the surface must remain flat. But if the pressure on one side of the surface differs from pressure on the other side, the pressure difference times the surface area results in a normal force. In order for the surface tension forces to cancel out this force due to pressure, the surface must be curved. When all the forces are balanced, the curvature of the surface is a good measure of the surface tension, which is described by the Young-Laplace equation:

$\Delta P = \gamma \left (\frac{1}{R_{1}}+\frac{1}{R_{2}} \right )$

where $\Delta P$ is the pressure differential across the interface, $\gamma$ is the measured surface tension, and $R_1, R_2$ are the principal radii of curvature, which indicate the degree of curvature.

This equation describes the shape and curvature of water bubbles and puddles, the "footprints" of water-walking insects, and the phenomenon of a needle floating on the surface of water. Even though the needle is denser than water, it floats because surface tension is a contractive tendency of the surface of a liquid that allows it to resist an external force. This property is caused by cohesion of similar molecules and is responsible for many of the behaviors of liquids.

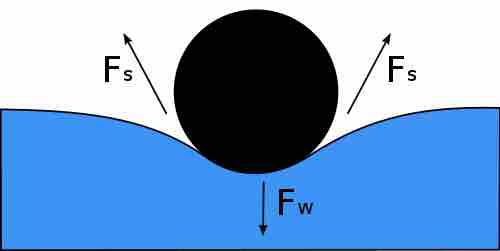
Resolution of forces on a "floating needle"

For a needle floating on the surface of a liquid, the downward force of the needle's weight is balanced by the upward forces of surface tension from the liquid. Note that the forces from the surface tension are symmetrical.

Potential Energy of Molecules in a Liquid

In imagining the shape of a liquid droplet or the curvature of the surface of a liquid, one must keep in mind that the molecules at the surface are at a different level of potential energy than are those of the interior. That is to say, there is an energy difference between the interior and the surface: to move a molecule from the interior to the surface requires energy. Liquids (for instance, in the form of a droplet) are shaped in a way that minimizes the energy at the surface. Again, since the energy at the surface is due in large part to the intermolecular attractive forces between particles on the surface and those in the interior, the surface tension is an indicator of the extent of those forces. Different liquids and solutions have different surface tensions.

The surface tensions of a few common liquids and solutions are as follows, in dyne/cm (note the particularly high surface tension of water):

• water, H(OH): 72.7
• benzene, C₆H₆: 40.0
• glycerin, C₃H₂(OH)₃: 63.0
• sucrose solution (85% in water): 76.4

Units of Surface Tension

Surface tension is expressed in units of force per unit length or of energy per unit area (for instance, N/m or J/m²). The two are equivalent, but when referring to energy per unit area, people use the term "surface energy," which is a more general term in the sense that it applies to solids as well as to liquids.

An example of surface tension

Water striders can "walk" on water as a result surface tension.