Quantum indeterminacy refers to the necessary incompleteness in the description of a physical system. Indeterminacy has become one of the characteristics of the standard description of quantum physics. Quantum indeterminacy can be quantitatively characterized by a probability distribution on the set of outcomes for measurements of an observable. This distribution is uniquely determined by the system state. Quantum mechanics provides a recipe for calculating this probability distribution.
An adequate account of quantum indeterminacy requires a theory of measurement. Many theories have been proposed since the beginning of quantum mechanics, and quantum measurement continues to be an active research area in both theoretical and experimental physics. Possibly the first systematic attempt at a mathematical theory for quantum measurement was developed by John von Neumann. The measurements he investigated are now called projective measurements.
Quantum indeterminacy can be illustrated in terms of a particle with a definitely measured momentum for which there must be a fundamental limit to how precisely its location can be specified. This quantum uncertainty principle can also be expressed in terms of other variables. For example, a particle with a definitely measured energy has a fundamental limit to how precisely one can specify how long it will have that energy.
Therefore the units involved in quantum uncertainty are on the order of Planck's constant (found experimentally to be 6.6 x 10−34 J·s).
Quantum indeterminacy is the assertion that the state of a system does not determine a unique collection of values for all its measurable properties. In quantum mechanical formalism, it is impossible that, for a given quantum state, each one of these measurable properties (observables) has a determinate (sharp) value. The values of an observable will be obtained non-deterministically in accordance with a probability distribution uniquely determined by the system state. The state is destroyed by measurement, so each measured value in a collection must be obtained using a freshly prepared state.
Classical Particles
According to classical physics, particles move in a very specific trajectory that is completely determined by the particle's velocity, position, and the sum of any forces acting on it. In the classical sense, these are known and repeatable. A bullet propelled from a gun at a consistent velocity under identical conditions will always follow the same trajectory and hit the same target. The bullet follows Newton's laws of motion, in whichthe present determines the future. Newton's laws are deterministic.
Quantum Particles
In the world of quantum phenomena, this is not the case. Recall from the uncertainty principle that we cannot simultaneously know an electron's position and velocity—therefore we are unable to determine its trajectory. Since either its present position or velocity is unknown, we cannot know where it will be with any certainty after a known time interval. This is called indeterminacy. We do know where it could be. Based on numerous observations, the quantum state, and the wave equation for the electron, we can determine a statistical map of probable positions for the electron. This is called a probability distribution map, a statistical representation of the probable locations of electrons as they exist in an atom.
The clouds of probability are the locations of electrons as determined by making repeated measurements—each measurement finds the electron in a definite location, with a greater chance of finding the electron in some places rather than others. With repeated measurements, a pattern of probability emerges. The clouds of probability do not look like nor do they correspond to classical orbits. The uncertainty principle prevents us from knowing how the electron gets from one place to another, and so an orbit really does not exist as such. Nature on a small scale is much different from that on the large scale.
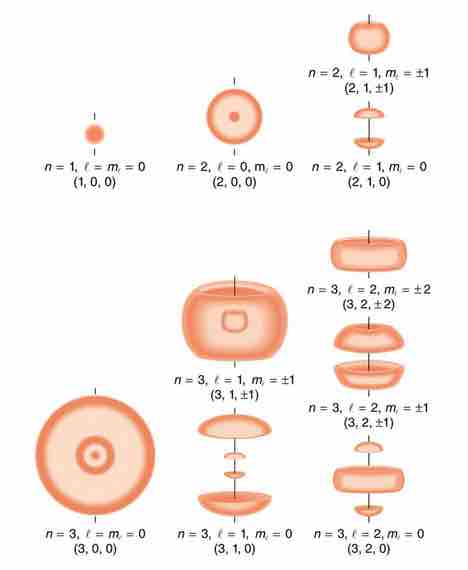
Probability density of hydrogen electrons
As indicated by the quantum numbers (n, l, ml), this figure depicts probability clouds for the electron in the ground state and several excited states of hydrogen.