Second-Order Reactions

A reaction is said to be second-order when the overall order is two. For a reaction with the general form $aA+bB\rightarrow C$, the reaction can be second order in two possible ways. It can be second-order in either A or B, or first-order in both A and B. If the reaction were second-order in either reactant, it would lead to the following rate laws:

$rate=k[A]^2$

or

$rate=k[B]^2$

The second scenario, in which the reaction is first-order in both A and B, would yield the following rate law:

$rate=k[A][B]$

Applying the Method of Initial Rates to Second-Order Reactions

Consider the following set of data:

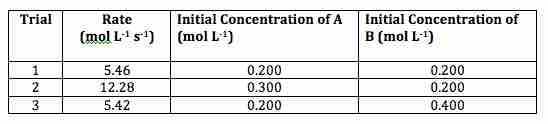
Rates and initial concentrations for A and B

A table showing data for three trials measuring the various rates of reaction as the initial concentrations of A and B are changed.

If we are interested in determining the order of the reaction with respect to A and B, we apply the method of initial rates.

Determining Reaction Order in A

In order to determine the reaction order for A, we can set up our first equation as follows:

$\frac{r_1}{r_2}=\frac{k[A]_1^x[B]_1^y}{k[A]_2^x[B]_2^y}$

$\frac{5.46}{12.28}=\frac{k(0.200)^x(0.200)^y}{k(0.300)^x(0.200)^y}$

Note that on the right side of the equation, both the rate constant k and the term $(0.200)^y$ cancel. This was done intentionally, because in order to determine the reaction order in A, we need to choose two experimental trials in which the initial concentration of A changes, but the initial concentration of B is constant, so that the concentration of B cancels. Our equation simplifies to:

$\frac{5.46}{12.28}=\frac{(0.200)^x}{(0.300)^x}$

$0.444=\left(\frac{2}{3}\right)^x$

$ln(0.444)=x\cdot ln\left(\frac{2}{3}\right)$

$x\approx 2$

Therefore, the reaction is second-order in A.

Determining Reaction Order in B

Next, we need to determine the reaction order for B. We do this by picking two trials in which the concentration of B changes, but the concentration of A does not. Trials 1 and 3 will do this for us, and we set up our ratios as follows:

$\frac{r_1}{r_3}=\frac{k[A]_1^2[B]_1^y}{k[A]_3^2[B]_3^y}$

$\frac{5.46}{5.42}=\frac{k(0.200)^2(0.200)^y}{k(0.200)^2(0.400)^y}$

Note that both k and the concentrations of A cancel. Also, $\frac{5.46}{5.42}\approx 1$, so everything simplifies to:

$1=\frac{(0.200)^y}{(0.400)^y}$

$1=\left(\frac{1}{2}\right)^y$

$y=0$

Therefore, the reaction is zero-order in B.

Overall Reaction Order

We have determined that the reaction is second-order in A, and zero-order in B. Therefore, the overall order for the reaction is second-order $(2+0=2)$, and the rate law will be:

$rate=k[A]^2$