Diprotic and Polyprotic Acids

Diprotic and polyprotic acids contain multiple acidic protons that dissociate in distinct, sequential steps.

Learning Objective

Identify the key features that distinguish polyprotic acids from monoprotic acids.

Key Points

Polyprotic acids can lose two or more acidic protons; diprotic acids and triprotic acids are specific types of polyprotic acids that can lose two and three protons, respectively.
Polyprotic acids display as many equivalence points in titration curves as the number of acidic protons they have; for instance, a diprotic acid would have two equivalence points, while a triprotic acid would have three equivalence points.
For polyprotic acids, the first Ka is always the largest, followed by the second, etc.; this indicates that the protons become successively less acidic as they are lost.
Although the tendency to lose each acidic proton decreases as subsequent ones are lost, all possible ionic species do exist in solution; to calculate their fractional concentration, one can use equations that rely on equilibrium constants and the concentration of protons in solution.

Terms

triprotic acid
one that can donate three hydrogen ions per molecule during dissociation
diprotic acid
one that contains within its molecular structure two hydrogen atoms per molecule capable of dissociating
equivalence point
the point at which an added titrant is stoichiometrically equal to the number of moles in a sample's substance; the smallest amount of titrant necessary to fully neutralize or react with the analyte
titration
determining a substance's concentration in a solution by slowly adding measured amounts of another substance (often with a burette) until a reaction is shown complete

Full Text

As their name suggests, polyprotic acids contain more than one acidic proton. Two common examples are carbonic acid (H₂CO₃, which has two acidic protons and is therefore a diprotic acid) and phosphoric acid (H₃PO₄, which has three acidic protons and is therefore a triprotic acid).

Diprotic and polyprotic acids show unique profiles in titration experiments, where a pH versus titrant volume curve clearly shows two equivalence points for the acid; this is because the two ionizing hydrogens do not dissociate from the acid at the same time. With any polyprotic acid, the first amd most strongly acidic proton dissociates completely before the second-most acidic proton even begins to dissociate.

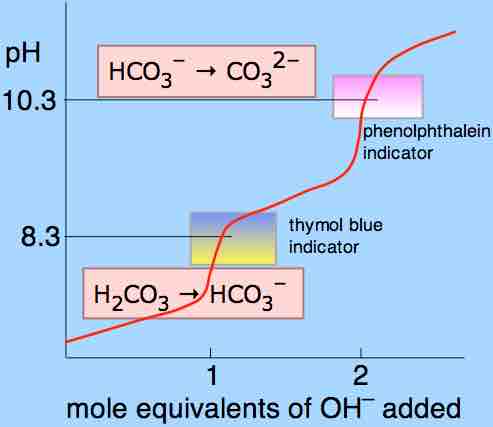
Titration curve of carbonic acid

The titration curve of a polyprotic acid has multiple equivalence points, one for each proton. In carbonic acid's case, the two ionizing protons each have a unique equivalence point.

Diprotic Acids

A diprotic acid (here symbolized by H₂A) can undergo one or two dissociations depending on the pH. Dissociation does not happen all at once; each dissociation step has its own K_a value, designated K_a1 and K_a2:

$H_2A(aq) \rightleftharpoons H^+(aq) + HA^-(aq) \quad\quad K_{a1}$

$HA^-(aq) \rightleftharpoons H^+(aq) + A^{2-}(aq)\quad\quad K_{a2}$

The first dissociation constant is necessarily greater than the second ( i.e. K_a1 > K_a2); this is because the first proton to dissociate is always the most strongly acidic, followed in order by the next most strongly acidic proton. For example, sulfuric acid (H₂SO₄) can donate two protons in solution:

$H_2SO_4(aq)\rightarrow H^+(aq)+HSO_4^-(aq)\quad\quad K_{a1}=\text{large}$

$HSO_4^-(aq)\rightleftharpoons H^+(aq)+SO_4^-(aq)\quad\quad K_{a2}=\text{small}$

This first dissociation step of sulfuric acid will occur completely, which is why sulfuric acid is considered a strong acid; the second dissociation step is only weakly dissociating, however.

Triprotic Acids

A triprotic acid (H₃A) can undergo three dissociations and will therefore have three dissociation constants: K_a1> K_a2 > K_a3.Take, for example the three dissociation steps of the common triprotic acid phosphoric acid:

$H_3PO_4(aq)\rightarrow H^+(aq)+H_2PO_4^-(aq)\quad\quad K_{a1}=large$

$H_2PO_4^-(aq)\rightleftharpoons H^+(aq)+HPO_4^{2-}(aq)\quad\quad K_{a2}=small$

$HPO_4^{2-}\rightleftharpoons H^+(aq)+PO_4^{3-}(aq)\quad\quad K_{a3}=smallest$

Fractional Concentration of Conjugate Base Species

Although the subsequent loss of each hydrogen ion is less favorable, all of a polyprotic acid's conjugate bases are present to some extent in solution. Each species' relative level is dependent on the pH of the solution. Given the pH and the values of K_a for each dissociation step, we can calculate each species' fractional concentration, α (alpha). The fractional concentration is defined as the concentration of a particular conjugate base of interest, divided by the sum of all species' concentrations. For example, a generic diprotic acid will generate three species in solution: H₂A, HA^-, and A^2-, and the fractional concentration of HA^-, which is given by:

$\alpha=\frac{[HA^-]}{[H_2A]+[HA^-]+[A^{2-}]}$

The following formula shows how to find this fractional concentration of HA^-, in which pH and the acid dissociation constants for each dissociation step are known:

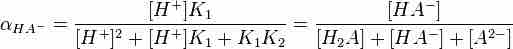
Fractional ion calculations for polyprotic acids

The above complex equations can determine the fractional concentration of various ions from polyprotic acids.

[ edit ]

Prev Concept

Base Dissociation Constant

Calculating Equilibrium Concentrations of Polyprotic Acids

Next Concept