Tips for Testing Series

Convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence, or divergence of an infinite series. When testing the convergence of a series, you should remember that there is no single convergence test which works for all series. It is up to you to guess and pick the right test for a given series. Practice and training will help you in expediting this "guessing" process.

Here is a summary for the convergence test that we have learned:

List of Tests

Limit of the Summand: If the limit of the summand is undefined or nonzero, then the series must diverge.

Ratio test: For $r = \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right|$, if $r < 1$, the series converges; if $r > 1$, the series diverges; if $r = 1$, the test is inconclusive.

Root test: For $r = \limsup_{n \to \infty}\sqrt[n]{ \left|a_n \right|}$, if $r < 1$, then the series converges; if $r > 1$, then the series diverges; if $r = 1$, the root test is inconclusive.

Integral test: For a positive, monotone decreasing function $f(x)$ such that $f(n)=a_n$, if $\int_{1}^{\infty} f(x)\, dx = \lim_{t \to \infty} \int_{1}^{t} f(x)\, dx < \infty$ then the series converges. But if the integral diverges, then the series does so as well.

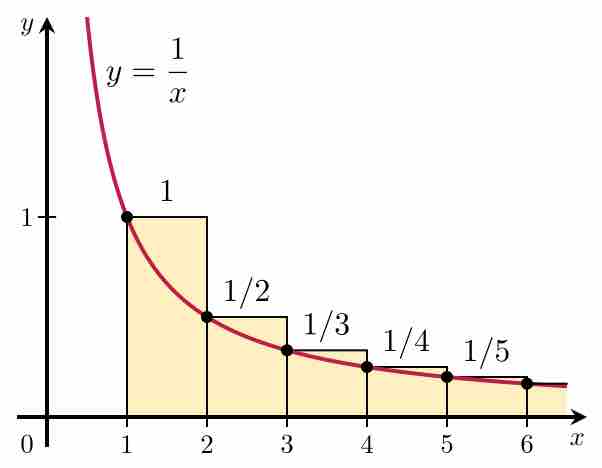
Integral Test

The integral test applied to the harmonic series. Since the area under the curve $y = \frac{1}{x}$ for $x \in [1, ∞)$ is infinite, the total area of the rectangles must be infinite as well.

Direct comparison test: If the series $\sum_{n=1}^\infty b_n$ is an absolutely convergent series and $\left |a_n \right | \le \left | b_n \right|$ for sufficiently large $n$, then the series $\sum_{n=1}^\infty a_n$ converges absolutely.

Limit comparison test: If $\left \{ a_n \right \}, \left \{ b_n \right \} > 0$, and $\lim_{n \to \infty} \frac{a_n}{b_n}$ exists and is not zero, then $\sum_{n=1}^\infty a_n$ converges if and only $if \sum_{n=1}^\infty b_n$ converges.