Differential equations are very important in the mathematical modeling of physical systems.
Many fundamental laws of physics and chemistry can be formulated as differential equations. In biology and economics, differential equations are used to model the behavior of complex systems. The mathematical theory of differential equations first developed together with the sciences where the equations had originated and where the results found application. However, diverse problems, sometimes originating in quite distinct scientific fields, may give rise to identical differential equations. Whenever this happens, mathematical theory behind the equations can be viewed as a unifying principle behind diverse phenomena. As an example, consider propagation of light and sound in the atmosphere, and of waves on the surface of a pond. All of them may be described by the same second-order partial-differential equation, the wave equation, which allows us to think of light and sound as forms of waves, much like familiar waves in the water. Conduction of heat is governed by another second-order partial differential equation, the heat equation .
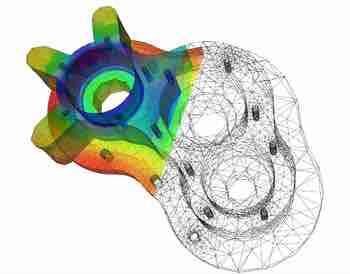
Visual Model of Heat Transfer
Visualization of heat transfer in a pump casing, created by solving the heat equation. Heat is being generated internally in the casing and being cooled at the boundary, providing a steady state temperature distribution.
A good example of a physical system modeled with differential equations is radioactive decay in physics.
Over time, radioactive elements decay. The half-life,
We can combine these quantities in a differential equation to determine the activity of the substance. For a number of radioactive particles
a first-order differential equation.