The logistic function is the solution of the following simple first-order non-linear differential equation:
with boundary condition
The derivative is
Choosing the constant of integration
More quantitatively, as can be seen from the analytical solution, the logistic curve shows early exponential growth for negative
The logistic equation is commonly applied as a model of population growth, where the rate of reproduction is proportional to both the existing population and the amount of available resources, all else being equal. The equation describes the self-limiting growth of a biological population.
Letting
where the constant
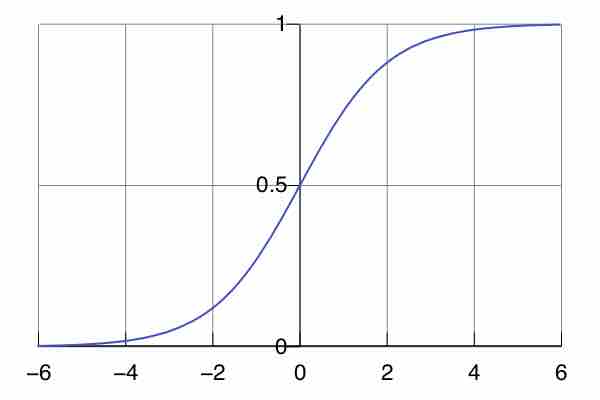
Logistic Curve
The standard logistic curve. It can be used to model population growth because of the limiting effect scarcity has on the growth rate. This is represented by the ceiling past which the function ceases to grow.