Volumes of Revolution

A solid of revolution is a solid figure obtained by rotating a plane curve around some straight line (the axis) that lies on the same plane . Here, we will study how to compute volumes of these objects. Two common methods for finding the volume of a solid of revolution are the disc method and the shell method of integration. To apply these methods, it is easiest to draw the graph in question; identify the area that is to be revolved about the axis of revolution; determine the volume of either a disc-shaped slice of the solid, with thickness $\delta x$, or a cylindrical shell of width $\delta x$; and then find the limiting sum of these volumes as $\delta x$ approaches $0$, a value which may be found by evaluating a suitable integral.

A Volume of Revolution

A solid formed by rotating a curve around an axis.

Disc Method

The disc method is used when the slice that was drawn is perpendicular to the axis of revolution; i.e. when integrating parallel to the axis of revolution. The volume of the solid formed by rotating the area between the curves of $f(x)$ and $g(x)$ and the lines $x=a$ and $x=b$ about the $x$-axis is given by: 

$\displaystyle{V = \pi \int_a^b \left | f^2(x) - g^2(x) \right | \,dx}$

If $g(x) = 0$ (e.g. revolving an area between curve and $x$-axis), this reduces to: 

$\displaystyle{V = \pi \int_a^b f(x)^2 \,dx}$

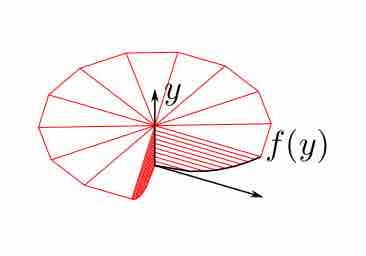
Disc Integration

Disc integration about the $y$-axis. Integration is along the axis of revolution ($y$-axis in this case).

The method can be visualized by considering a thin horizontal rectangle at $y$between $y=f(x)$ on top and $y=g(x)$ on the bottom, and revolving it about the $y$-axis; it forms a ring (or disc in the case that $g(x)=0$), with outer radius $f(x)$ and inner radius $g(x)$. The area of a ring is:

 $\pi (R^2 - r^2)$

where $R$ is the outer radius (in this case $f(x)$), and $r$ is the inner radius (in this case $g(x)$). Summing up all of the areas along the interval gives the total volume. Alternatively, where each disc has a radius of $f(x)$, the discs approach perfect cylinders as their height $dx$ approaches zero. The volume of each infinitesimal disc is therefore:

 $\pi f^2(x) dx$

An infinite sum of the discs between $a$ and $b$ manifests itself as the integral seen above, replicated here:

$\displaystyle{V = \pi \int_a^b f(x)^2 \,dx}$

Shell Method

The shell method is used when the slice that was drawn is parallel to the axis of revolution; i.e. when integrating perpendicular to the axis of revolution. The volume of the solid formed by rotating the area between the curves of $f(x)$and $g(x)$ and the lines $x=a$ and $x=b$ about the $y$-axis is given by:

$\displaystyle{V = 2\pi \int_a^b x \left | f(x) - g(x) \right | \,dx}$

If $g(x)=0$ (e.g. revolving an area between curve and $x$-axis), this reduces to:

 $\displaystyle{V = 2\pi \int_a^b x \left | f(x) \right | \,dx}$

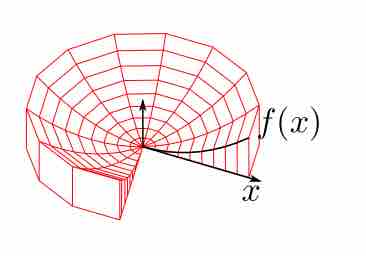
Shell Integration

The integration (along the $x$-axis) is perpendicular to the axis of revolution ($y$-axis).

The method can be visualized by considering a thin vertical rectangle at $x$ with height $[f(x)-g(x)]$ and revolving it about the $y$-axis; it forms a cylindrical shell. The lateral surface area of a cylinder is $2 \pi r h$, where $r$ is the radius (in this case $x$), and $h$ is the height (in this case $[f(x)-g(x)]$). Summing up all of the surface areas along the interval gives the total volume.