Shell integration (also called the shell method) is a means of calculating the volume of a solid of revolution when integrating perpendicular to the axis of revolution . (When integrating parallel to the axis of revolution, you should use the disk method. ) While less intuitive than disk integration, it usually produces simpler integrals. Intuitively speaking, part of the graph of a function is rotated around an axis, and is modeled by an infinite number of cylindrical shells, all infinitely thin.
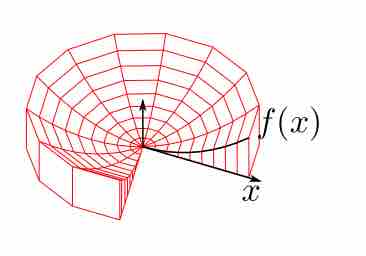
The Shell Method
Calculating volume using the shell method. Each segment located at
The idea is that a "representative rectangle" (used in the most basic forms of integration, such as
The volume of the solid formed by rotating the area between the curves of
In the integrand, the factor
The volume of solid formed by rotating the area between the curves of