Trigonometric Functions

Trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle. Trigonometric functions are important in the study of triangles and modeling periodic phenomena, among many other applications.

The most familiar trigonometric functions are the sine, cosine, and tangent . In the context of the standard unit circle with radius 1, where a triangle is formed by a ray originating at the origin and making some angle with the x-axis, the sine of the angle gives the length of the y-component (rise) of the triangle, the cosine gives the length of the x-component (run), and the tangent function gives the slope (y-component divided by the x-component) .

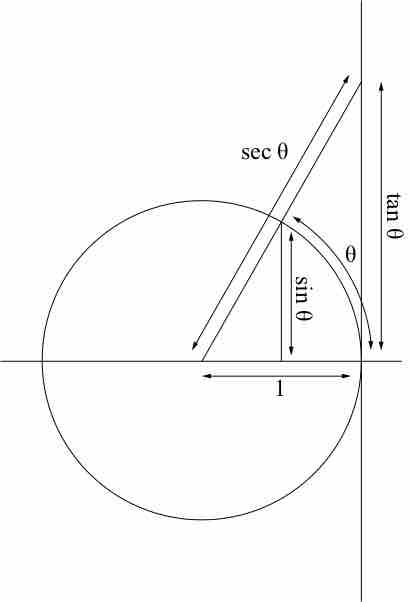
Sine, Tangent, and Secant

The sine, tangent, and secant functions of an angle constructed geometrically in terms of a unit circle. The number θ is the length of the curve; thus angles are being measured in radians.

Base of Trigonometry

If two right triangles have equal acute angles, they are similar, so their side lengths are proportional. Proportionality constants are written within the image: $\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$ where $\theta$ is the common measure of five acute angles.

Trigonometric functions are commonly defined as ratios of two sides of a right triangle containing the angle, and can equivalently be defined as the lengths of various line segments from a unit circle. More modern definitions express them as infinite series or as solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers.

Right-angle Triangle Definitions

The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case $\sin A = \frac {\textrm{opposite}} {\textrm{hypotenuse}} = \frac {a} {h}$ . Note that this ratio does not depend on size of the particular right triangle chosen, as long as it contains the angle $A$, since all such triangles are similar.

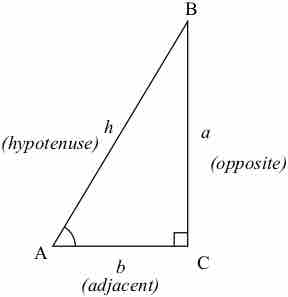
Right-Angle Triangle

Right-angle triangle used in defining trigonometric functions.

The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse: so called because it is the sine of the complementary or co-angle. In our case $\cos A = \frac {\textrm{adjacent}} {\textrm{hypotenuse}} = \frac {b} {h}$.

The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side: so called because it can be represented as a line segment tangent to the circle, that is the line that touches the circle, from Latin linea tangens or touching line (cf. tangere, to touch). In our case $\tan A = \frac {\textrm{opposite}} {\textrm{adjacent}} = \frac {a} {b}$.