Limits of functions can often be determined using simple laws. In this atom, we will study two examples: L'Hôpital's rule or the squeeze theorem.
L'Hôpital's Rule
L'Hôpital's rule (pronounced "lope-ee-tahl," sometimes spelled l'Hospital's rule with silent "s" and identical pronunciation), also called Bernoulli's rule, uses derivatives to help evaluate limits involving indeterminate forms. Application (or repeated application) of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit.
In its simplest form, l'Hôpital's rule states that if functions
-
$\displaystyle{\lim_{x \to c}f(x)=\lim_{x \to c}g(x)=0 \text{ or } \pm\infty}$ -
$\displaystyle{\lim_{x\to c}\frac{f'(x)}{g'(x)}}$ exists, - and, if and only if
$g'(x)\neq 0 \text{ for all } x \text{ in } I \text{ } (x \neq c)$ , THEN$\displaystyle{\lim_{x\to c}\frac{f(x)}{g(x)} = \lim_{x\to c}\frac{f'(x)}{g'(x)}}$ .
The differentiation of the numerator and denominator often simplifies the quotient and/or converts it to a determinate form, allowing the limit to be evaluated more easily.
The Squeeze Theorem
The squeeze theorem is a technical result that is very important in proofs in calculus and mathematical analysis. It is typically used to confirm the limit of a function via comparison with two other functions whose limits are known or easily computed. The squeeze theorem is formally stated as follows:
Let
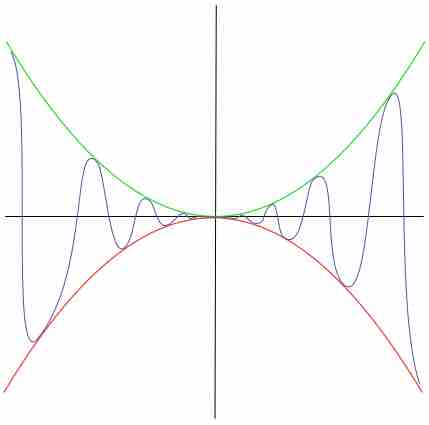
Squeeze Theorem