Lagrange Multiplers

In mathematical optimization, the method of Lagrange multipliers (named after Joseph Louis Lagrange) is a strategy for finding the local maxima and minima of a function subject to equality constraints.

For instance, consider the following optimization problem: Maximize $f(x,y)$ subject to $g(x,y)=c$. We need both $f$ and $g$ to have continuous first partial derivatives. We introduce a new variable ($\lambda$) called a Lagrange multiplier, and study the Lagrange function (or Lagrangian) defined by:

$\Lambda(x,y,\lambda) = f(x,y) + \lambda \cdot \left(g(x,y)-c\right)$

where the $\lambda$ term may be either added or subtracted. If $f(x_0, y_0)$ is a maximum of $f(x,y)$ for the original constrained problem, then there exists $\lambda_0$ such that $(x_0,y_0,\lambda_0)$ is a stationary point for the Lagrange function (stationary points are those points where the partial derivatives of $\Lambda$ are zero, i.e., $\nabla\Lambda = 0$). However, not all stationary points yield a solution of the original problem. Thus, the method of Lagrange multipliers yields a necessary condition for optimality in constrained problems. Sufficient conditions for a minimum or maximum also exist.

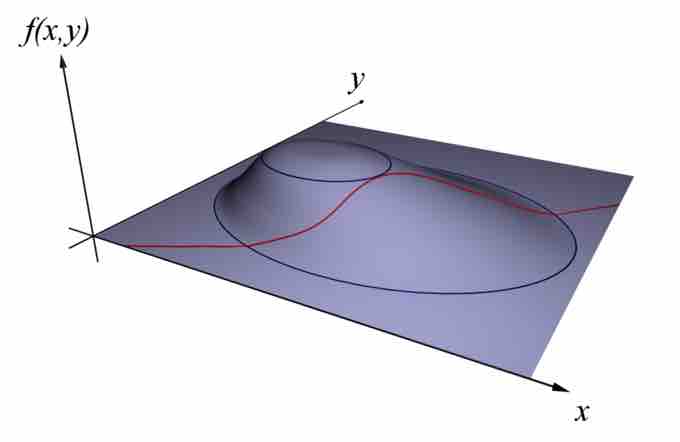
Maximizing f(x,y)

Find x and y to maximize f(x,y) subject to a constraint (shown in red) g(x,y)=c.

Introduction

One of the most common problems in calculus is that of finding maxima or minima (in general, "extrema") of a function, but it is often difficult to find a closed form for the function being extremized. Such difficulties often arise when one wishes to maximize or minimize a function subject to fixed outside conditions or constraints. The method of Lagrange multipliers is a powerful tool for solving this class of problems without the need to explicitly solve the conditions and use them to eliminate extra variables.

Consider the two-dimensional problem introduced above. Maximize $f(x,y)$ subject to $g(x,y)=c$. We can visualize contours of $f$ given by $f(x, y)=d$ for various values of $d$, and the contour of $g$ given by $g (x, y) = c$. Suppose we walk along the contour line with $g = c$. In general, the contour lines of $f$ and $g$ may be distinct, so following the contour line for $g = c$, one could intersect with or cross the contour lines of $f$. This is equivalent to saying that while moving along the contour line for $g = c$, the value of $f$ can vary. When the contour line for $g = c$ meets contour lines of $f$ tangentially we neither increase nor decrease the value of $f$—that is, when the contour lines touch but do not cross.

The contour lines of $f$ and $g$ touch when the tangent vectors of the contour lines are parallel. Since the gradient of a function is perpendicular to the contour lines, this is the same as saying that the gradients of $f$ and $g$ are parallel. Thus, we want points:

$(x,y)$ where $g(x,y)=c$

and

$\nabla_{x,y} f = - \lambda \nabla_{x,y} g$, where $\nabla_{x,y} f= \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$ and $\nabla_{x,y} g= \left( \frac{\partial g}{\partial x}, \frac{\partial g}{\partial y} \right)$ are the respective gradients. 

The constant is required because, although the two gradient vectors are parallel, the magnitudes of the gradient vectors are generally not equal. Note that $\lambda \neq 0$; otherwise we cannot assert the two gradients are parallel.

To incorporate these conditions into one equation, we introduce an auxiliary function, $\Lambda(x,y,\lambda) = f(x,y) + \lambda \cdot \Big(g(x,y)-c\Big)$, and solve $\nabla_{x,y,\lambda} \Lambda(x , y, \lambda)=0$. This is the method of Lagrange multipliers. Note that $\nabla_{\lambda} \Lambda(x , y, \lambda)=0$ implies $g(x,y)=c$.

Where the Lagrange multiplier $\lambda=0$ we can have a local extremum and the two contours cross instead of meeting tangentially. Consider the following example.

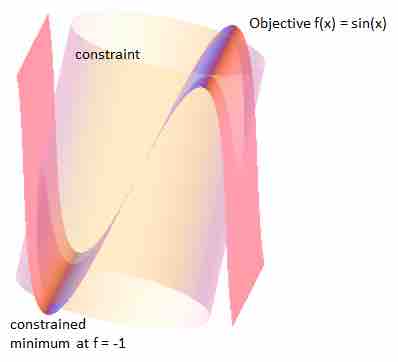
Minimize $f(x,y) = \sin(x)$, given that $g(x,y) = x^2 + y^2=9$. Every point $\left(\frac{-\pi}{2}, y\right)$$f=-1$ is a global minimum of $f$ with value $-1$. Therefore where the constraint $g=c$ crosses the contour line $f=-1$, is a local minimum of $f$ on the constraint. The trace and the contour $f=-1$ cross at the minimum as we can see in the figure. It is easy to verify that $f_x=0$  and $f_y=0$ when $x = \frac{\pi}{2}$. Since both $g_x \neq 0$ and $g_y \neq 0$, the Lagrange multiplier $\lambda = 0$ at the minimum.

Example where the contour and constraint cross at an extremum.