Symmetry in Trigonometric Functions
We have previously discussed even and odd functions. Recall that even functions are symmetric about the
We will now consider each of the trigonometric functions and their cofunctions (secant, cosecant, and cotangent), and observe symmetry in their graphs. This symmetry is used to derive certain identities.
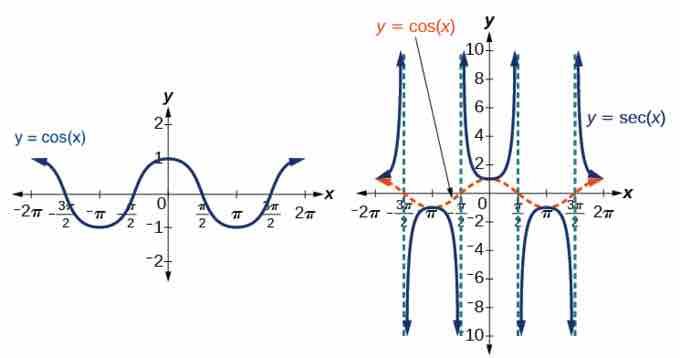
Symmetry around the $y$ -axis
Cosine and secant are even functions, with symmetry around the
The cosine and secant functions are symmetric about the y-axis.
Graphs that are symmetric about the

Symmetry around the origin
Sine, cosecant, tangent, and cotangent are odd functions, and are symmetric around the origin.
The sine, cosecant, tangent, and cotangent functions are symmetric about the origin.
Graphs that are symmetric about the origin represent odd functions. For odd functions, any two points with opposite
Symmetry Identities
We can apply the definitions for even and odd functions to derive symmetry identities that correspond to each of our six trigonometric functions. The following symmetry identities are useful in finding the trigonometric function of a negative value.
Notice that only two of the trigonometric identities are even functions: cosine and secant. For these functions, we apply
For the odd trigonometric functions, we apply
Example
Find the sine, cosine, and tangent of
First, we can identify that the absolute value of
Using these values from the unit circle, we can calculate
Now that we know the sine, cosine, and tangent of
Applying the symmetry identity for cosine, we have:
Applying the identity for sine, we have:
Finally, applying the identity for tangent, we have: