Trigonometric Functions of Special Angles

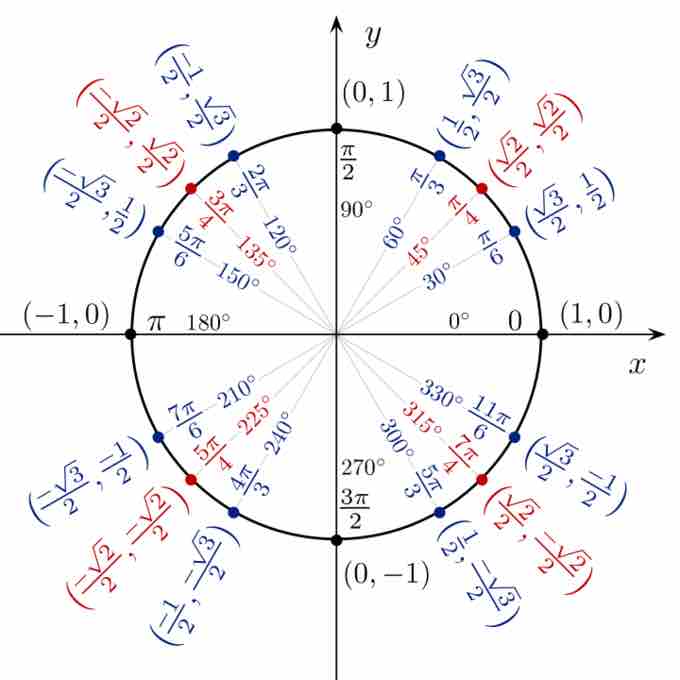
Recall that certain angles and their coordinates, which correspond to $x = \cos t$ and $y = \sin t$ for a given angle $t$, can be identified on the unit circle.

Unit circle

Special angles and their coordinates are identified on the unit circle.

The angles identified on the unit circle above have relatively simple expressions. Such simple expressions generally do not exist for other angles. Some examples of the algebraic expressions for the sines of special angles are:

$\displaystyle{ \begin{aligned} \sin{\left( 0^{\circ} \right)} &= 0 \\ \sin{\left( 30^{\circ} \right)} &= \frac{1}{2} \\ \sin{\left( 45^{\circ} \right)} &= \frac{\sqrt{2}}{2} \\ \sin{\left( 60^{\circ} \right)} &= \frac{\sqrt{3}}{2} \\ \sin{\left( 90^{\circ} \right)} &= 1 \\ \end{aligned} }$

The expressions for the cosine functions of these special angles are also simple. 

Note that while only sine and cosine are defined directly by the unit circle, tangent can be defined as a quotient involving these two:

$\displaystyle{ \tan t = \frac{\sin t}{\cos t} }$

Tangent functions also have simple expressions for each of the special angles. 

We can observe this trend through an example. Let's find the tangent of $60^{\circ}$.

First, we can identify from the unit circle that: 

$\displaystyle{ \begin{aligned} \sin{ \left(60^{\circ}\right) } &= \frac{\sqrt{3}}{2} \\ \cos{ \left(60^{\circ}\right) } &= \frac{1}{2} \end{aligned} }$

We can easily calculate the tangent: 

$\displaystyle{ \begin{aligned} \tan{\left(60^{\circ}\right)} &= \frac{\sin{\left(60^{\circ}\right)}}{\cos{\left(60^{\circ}\right)}} \\ &= \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} \\ &= \frac{\sqrt{3}}{2} \cdot \frac{2}{1} \\ &= \sqrt{3} \end{aligned} }$

Memorizing Trigonometric Functions 

An understanding of the unit circle and the ability to quickly solve trigonometric functions for certain angles is very useful in the field of mathematics. Applying rules and shortcuts associated with the unit circle allows you to solve trigonometric functions quickly. The following are some rules to help you quickly solve such problems.

Signs of Trigonometric Functions

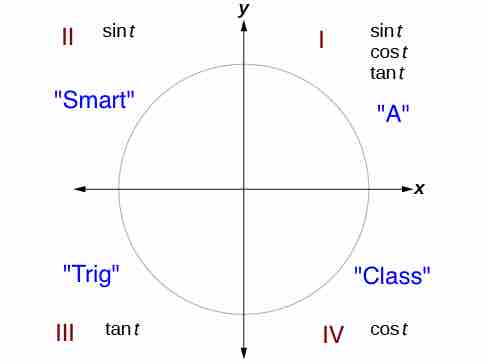
The sign of a trigonometric function depends on the quadrant that the angle falls in. To help remember which of the trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the trigonometric functions are positive. In quadrant II, “Smart,” only sine is positive. In quadrant III, “Trig,” only tangent is positive. Finally, in quadrant IV, “Class,” only cosine is positive. is positive.

Sign rules for trigonometric functions

The trigonometric functions are each listed in the quadrants in which they are positive.

Identifying Values using Reference Angles

Take a close look at the unit circle, and note that $\sin t$ and $\cos t$ take certain values as they fluctuate between $-1$ and $1$. You will notice that they take on the value of zero, as well as the positive and negative values of three particular numbers: $\displaystyle{\frac{\sqrt{3}}{2}}$, $\displaystyle{\frac{\sqrt{2}}{2}}$, and $\displaystyle{\frac{1}{2}}$. Identifying reference angles will help us identify a pattern in these values. 

Reference angles in quadrant I are used to identify which value any angle in quadrants II, III, or IV will take. This means that we only need to memorize the sine and cosine of three angles in quadrant I: $30^{\circ}$, $45^{\circ}$, and $60^{\circ}$.

For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the $y$-coordinate on the unit circle, the other angle with the same sine will share the same $y$-value, but have the opposite $x$-value. Therefore, its cosine value will be the opposite of the first angle’s cosine value.

Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. The angle with the same cosine will share the same $x$-value but will have the opposite $y$-value. Therefore, its sine value will be the opposite of the original angle’s sine value.

As shown in the diagrams below, angle $\alpha$ has the same sine value as angle $t$; the cosine values are opposites. Angle $\beta$ has the same cosine value as angle $t$; the sine values are opposites.

$\displaystyle{ \begin{aligned} \sin t = \sin \alpha \quad &\text{and} \quad \cos t = -\cos \alpha \\ \sin t = -\sin \beta \quad &\text{and} \quad \cos t = \cos \beta \end{aligned} }$

Reference angles

In the left figure, $t$ is the reference angle for $\alpha$. In the right figure, $t$ is the reference angle for $\beta$.

Recall that an angle’s reference angle is the acute angle, $t$, formed by the terminal side of the angle $t$ and the horizontal axis. A reference angle is always an angle between $0$ and $90^{\circ}$, or $0$ and $\displaystyle{\frac{\pi}{2}}$ radians. For any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

Reference angles in each quadrant

For any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

Thus, in order to recall any sine or cosine of a special angle, you need to be able to identify its angle with the $x$-axis in order to compare it to a reference angle. You will then identify and apply the appropriate sign for that trigonometric function in that quadrant. 

These are the steps for finding a reference angle for any angle between $0$ and $2\pi$:

1. An angle in the first quadrant is its own reference angle.
2. For an angle in the second or third quadrant, the reference angle is $|\pi - t|$ or $|180^{\circ} - t|$. 
3. For an angle in the fourth quadrant, the reference angle is $2\pi - t$ or $360^{\circ} - t$. If an angle is less than $0$ or greater than $2\pi$, add or subtract $2\pi$ as many times as needed to find an equivalent angle between $0$ and $2\pi$.

Since tangent functions are derived from sine and cosine, the tangent can be calculated for any of the special angles by first finding the values for sine or cosine.

Example

Find $\tan (225^{\circ})$, applying the rules above.

First, note that $225^{\circ}$ falls in the third quadrant:

Angle $225^{\circ}$ on a unit circle

The angle $225^{\circ}$falls in quadrant III.

Subtract $225^{\circ}$ from $180^{\circ}$ to identify the reference angle:

$\displaystyle{ \begin{aligned} \left| 180^{\circ} - 225^{\circ} \right| &= \left|-45^{\circ} \right| \\ &= 45^{\circ} \end{aligned} }$ 

In other words, $225^{\circ}$ falls $45^{\circ}$ from the $x$-axis. The reference angle is $45^{\circ}$. 

Recall that 

$\displaystyle{\sin{ \left(45^{\circ}\right)} = \frac{\sqrt{2}}{2} }$

However, the rules described above tell us that the sine of an angle in the third quadrant is negative. So we have 

$\displaystyle{\sin{ \left(225^{\circ}\right)} = -\frac{\sqrt{2}}{2} }$

Following the same process for cosine, we can identify that 

$\displaystyle{ \cos{ \left(225^{\circ}\right)} = -\frac{\sqrt{2}}{2} }$

We can find $\tan (225^{\circ})$ by dividing $\sin (225^{\circ})$ by $\cos (225^{\circ})$:

 $\displaystyle{ \begin{aligned} \tan{ \left(225^{\circ}\right)} &= \frac{\sin(225^{\circ})}{\cos (225^{\circ})} \\ &= \frac{-\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}} \\ &= -\frac{\sqrt{2}}{2} \cdot -\frac{2}{\sqrt{2}} \\ &= 1 \end{aligned} }$