Recall that a linear system may behave in any one of three possible ways:
- The system has a single unique solution.
- The system has no solution.
- The system has infinitely many solutions.
Also recall that each of these possibilities corresponds to a type of system of linear equations in two variables. An independent system of equations has exactly one solution
The previous modules have discussed how to find the solution for an independent system of equations. We will now focus on identifying dependent and inconsistent systems of linear equations.
Dependent Systems
The equations of a linear system are independent if none of the equations can be derived algebraically from the others. When the equations are independent, each equation contains new information about the variables, and removing any of the equations increases the size of the solution set. Systems that are not independent are by definition dependent. Equations in a dependent system can be derived from one another; they describe the same line. They do not add new information about the variables, and the loss of an equation from a dependent system does not change the size of the solution set.
We can apply the substitution or elimination methods for solving systems of equations to identify dependent systems. Dependent systems have an infinite number of solutions because all of
the points on one line are also on the other line. After using
substitution or addition, the resulting equation will be an identity,
such as
For example, consider the two equations
We can apply the elimination method to evaluate these. If we were to multiply the first equation by a factor of
Adding this to the second equation would yield
When graphed, the two equations produce identical lines, as demonstrated below.
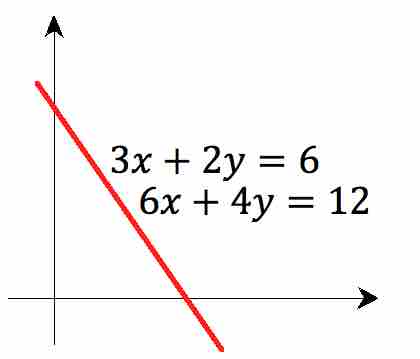
Dependent system
The equations
Note that there are an infinite number of solutions to a dependent system, and these solutions fall on the shared line.
Inconsistent Systems
A
linear system is consistent if it has a solution, and inconsistent
otherwise. Recall that the graphical representation of an inconsistent system consists of parallel lines that have the same slope but different
We can also apply methods for solving systems of equations to identify inconsistent systems. When the system is inconsistent, it is possible to derive a
contradiction from the equations, such as
the statement
Consider the following two equations:
We can apply the elimination method to attempt to solve this system. Subtracting the first equation from the
second one, both variables are eliminated and we get
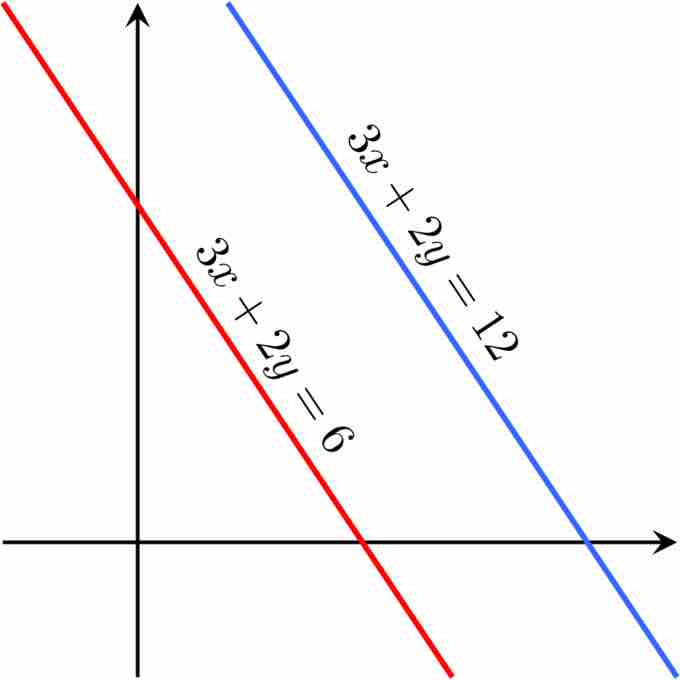
Inconsistent system
The equations 3x + 2y = 6 and 3x + 2y = 12 are inconsistent.
In general, inconsistencies occur if the left-hand sides of the equations in a system are linearly dependent, and the constant terms do not satisfy the dependence relation. A system of equations whose left-hand sides are linearly independent is always consistent.