Types of Asymptotes

In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity.

There are three kinds of asymptotes: horizontal, vertical and oblique. Horizontal asymptotes of curves are horizontal lines that the graph of the function approaches as $x$ tends to $+ \infty$ or $- \infty$. Horizontal asymptotes are parallel to the $x$-axis. 

Vertical asymptotes are vertical lines near which the function grows without bound. They are parallel to the $y$-axis. 

An asymptote that is neither horizontal or vertical is an oblique (or slant) asymptote. These are diagonal lines so that the difference between the curve and the line approaches $0$ as $x$ tends to $+ \infty$ or $- \infty$. 

Each type of asymptote is shown in the graph below.

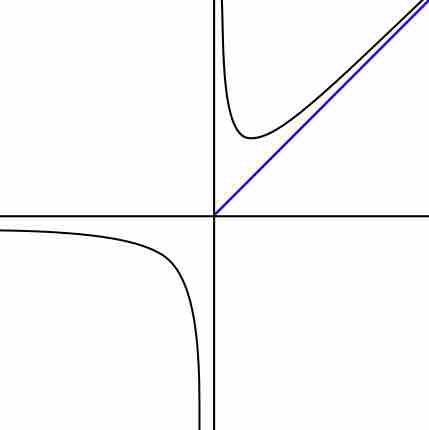
Graph with asymptotes

The graph of a function with a horizontal ($y=0$), vertical ($x=0$), and oblique asymptote (blue line).

Example 1

Consider the graph of the equation $f(x) = \frac {1}{x}$,  shown below. The coordinates of the points on the curve are of the form $(x, \frac {1}{x})$ where $x$ is a number other than 0. 

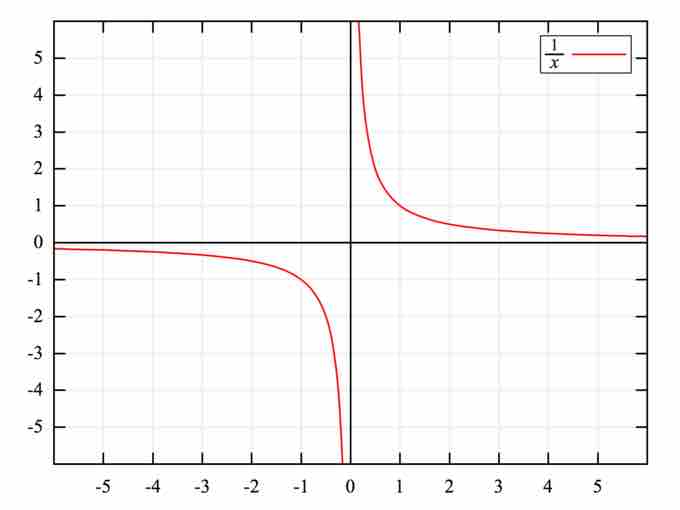
Graph of $f(x) = 1/x$

Both the $x$-axis and $y$-axis are asymptotes.

Notice that as the positive values of $x$ become larger and larger, the corresponding values of $y$ become infinitesimally small. However, no matter how large $x$ becomes, $\frac {1}{x}$ is never $0$, so the curve never actually touches the $x$-axis. The $x$-axis is a horizontal asymptote of the curve.

Similarly, as the positive values of $x$ become smaller and smaller, the corresponding values of $y$ become larger and larger. So the curve extends farther and farther upward as it comes closer and closer to the $y$-axis. The $y$-axis is a vertical asymptote of the curve. 

Asymptotes of Rational Functions

A rational function has at most one horizontal or oblique asymptote, and possibly many vertical asymptotes. 

Vertical asymptotes occur only when the denominator is zero. In other words, vertical asymptotes occur at singularities, or points at which the rational function is not defined. Vertical asymptotes only occur at singularities when the associated linear factor in the denominator remains after cancellation. 

For example, consider the function: 

$f(x) = \dfrac{(x-1)(x+2)}{(x-1)(x+1)}$ 

We can identify from the linear factors in the denominator that two singularities exist, at $x=1$ and $x = -1$. However, the linear factor $(x-1)$ cancels with a factor in the numerator. Thus, the only vertical asymptote for this function is at $x=-1$.

The degree of the numerator and degree of the denominator determine whether or not there are any horizontal or oblique asymptotes. 

Existence of horizontal asymptote depends on the degree of polynomial in the numerator ($n$) and degree of polynomial in the denominator ($m$). There are three possible cases:

1. If $n>m$, then there is no horizontal asymptote (However, if $n = m+1$, then there exists a slant asymptote).
2. If $n<m$, then the $x$-axis is a horizontal asymptote.
3. If $n=m$, then a horizontal asymptote exists, and the equation is:

$\quad \quad y = \frac{\text{Coefficient of highest power term in numerator}}{\text{Coefficient of highest power term in denominator}}$

When the numerator of a rational function has degree exactly one greater than the denominator, the function has an oblique (slant) asymptote. The asymptote is the polynomial term after dividing the numerator and denominator, and is a linear expression.

Example 2

Find any vertical asymptotes of

$f(x) = \dfrac{(x-1)(x+2)}{(x-1)^2(x+1)}$.

Notice that, based on the linear factors in the denominator, singularities exists at $x=1$ and $x=-1$. Also notice that one linear factor $(x-1)$ cancels with the numerator. However, one linear factor $(x-1)$ remains in the denominator because it is squared. Therefore, a vertical asymptote exists at $x=1$. The linear factor $(x + 1)$ also does not cancel out; thus, a vertical asymptote also exists at $x = -1$. 

Example 3

Find any horizontal or oblique asymptote of

$f(x) = \dfrac{2x^2 + x + 1}{x^2 + 16}$.

Because the polynomials in the numerator and denominator have the same degree ($2$), we can identify that there is one horizontal asymptote and no oblique asymptote.

The coefficient of the highest power term is $2$ in the numerator and $1$ in the denominator. Hence, horizontal asymptote is given by:

$y = \frac{2}{1} = 2$