If
General Definition and Process: Matrix Multiplication
Scalar multiplication is simply multiplying a value through all the elements of a matrix, whereas matrix multiplication is multiplying every element of each row of the first matrix times every element of each column in the second matrix. Scalar multiplication is much more simple than matrix multiplication; however, a pattern does exist.
When multiplying matrices, the elements of the rows in the first matrix are multiplied with corresponding columns in the second matrix. Each entry of the resultant matrix is computed one at a time.
For two matrices the final position of the product is shown below:
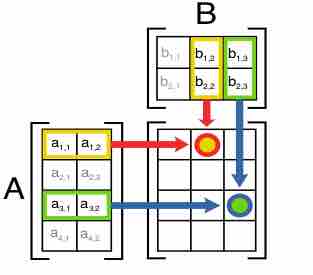
Matrix Multiplication
This figure illustrates diagrammatically the product of two matrices A and B, showing how each intersection in the product matrix corresponds to a row of A and a column of B.
The values at the intersections marked with circles are:
Matrix Multiplication: Process
Example 1: Find the product $AB$
First ask: Do the number of columns in
Start with producing the product for the first row, first column element. Take the first row of Matrix
Continue the pattern with the first row of
AB has entries defined by the equation: