The Distance Formula
In analytic geometry, the distance between two points of the
This formula is easily derived by constructing a right triangle with the hypotenuse connecting the two points (
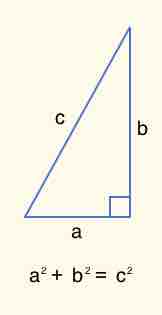
Pythagorean Theorem
The Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
The image below names the two points, with the distance between them as the variable,
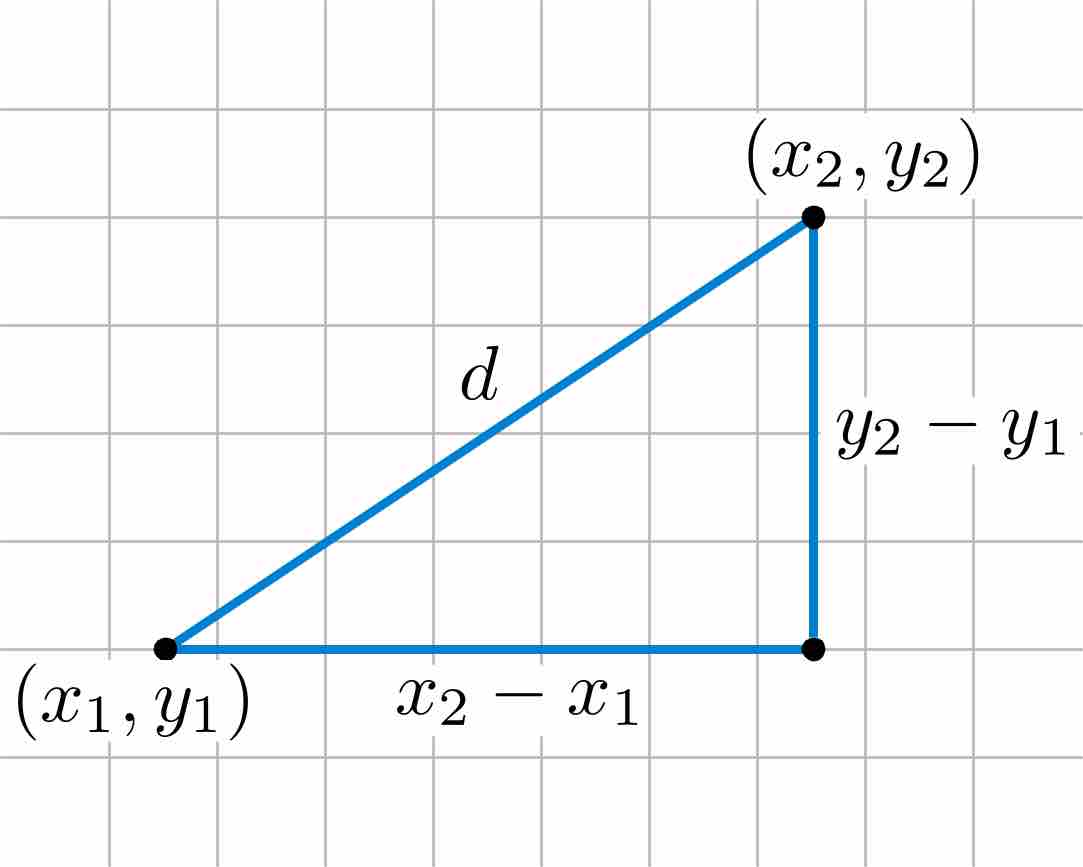
Distance Formula
The distance formula between two points,
Example: Find the distance between the points $(2,4)$ and $(5,8)$
Substitute the values into the distance formula that is derived from the Pythagorean Theorem:
Midpoint of a Line Segment
In geometry, the midpoint is the middle point of a line segment, or the middle point of two points on a line, and thus is equidistant from both end-points. If you have two points,
Another way to interpret this formula is an average: we average the
By looking at each coordinate, you can see that the
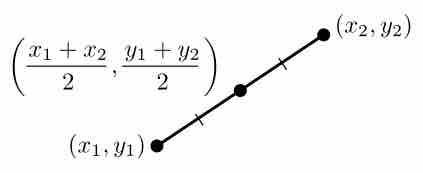
Midpoint of a Line Segment
The equation for a midpoint of a line segment with endpoints
Example: Find the midpoint between $(2,4) $ and $(5,8)$
Substitute the values into the midpoint formula: