Slope
In mathematics, the slope of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter
The direction of a line is either increasing, decreasing, horizontal or vertical.
A line is increasing if it goes up from left to right which implies that the slope is positive (
Slopes of Lines
The slope of a line can be positive, negative, zero, or undefined.
The steepness, or incline, of a line is measured by the absolute value of the slope. A slope with a greater absolute value indicates a steeper line. In other words, a line with a slope of
Calculating Slope
Slope is calculated by finding the ratio of the "vertical change" to the
"horizontal change" between any two distinct points on a line.
This ratio is represented by a quotient ("rise over run"), and gives
the same number for any two distinct points on the same line. It is represented by
Visualization of Slope
The slope of a line is calculated as "rise over run."
Mathematically, the slope m of the line is:
Two points on the line are required to find
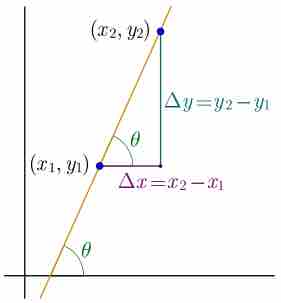
Slope Represented Graphically
The slope
Now we’ll look at some graphs on a coordinate grid to find their slopes. In many cases, we can find slope by simply counting out the rise and the run. We start by locating two points on the line. If possible, we try to choose points with coordinates that are integers to make our calculations easier.
Example
Find the slope of the line shown on the coordinate plane below.
Find the slope of the line
Notice the line is increasing so make sure to look for a slope that is positive.
Locate two points on the graph, choosing points whose coordinates are integers. We will use
Identify points on the line
Draw a triangle to help identify the rise and run.
Count the rise on the vertical leg of the triangle:
Count the run on the horizontal leg of the triangle:
Use the slope formula to take the ratio of rise over run:
The slope of the line is
Example
Find the slope of the line shown on the coordinate plane below.
Find the slope of the line
We can see the slope is decreasing, so be sure to look for a negative slope.
Locate two points on the graph. Look for points with coordinates that are integers. We can choose any points, but we will use
Identify two points on the line
The points
Apply the formula for slope:
Let
Plugging the corresponding values into the slope formula, we get:
The slope of the line is