Finding the present value (PV) of an amount of money is finding the amount of money today that is worth the same as an amount of money in the future, given a certain interest rate.
Calculating the present value (PV) of a single amount is a matter of combining all of the different parts we have already discussed. But first, you must determine whether the type of interest is simple or compound interest. If the interest is simple interest, you plug the numbers into the simple interest formula.

Simple Interest Formula
Simple interest is when interest is only paid on the amount you originally invested (the principal). You don't earn interest on interest you previously earned.
If it is compound interest, you can rearrange the compound interest formula to calculate the present value.
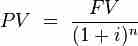
Present Value Single Payment
Finding the PV is a matter of plugging in for the three other variables.
Inputs
- Future Value: The known value of the money at a declared point in the future.
- Interest Rate (Discount Rate): Represented as either i or r. This is the percentage of interest paid each period.
- Number of periods: Represented as n or t.
Once you know these three variables, you can plug them into the appropriate equation. If the problem doesn't say otherwise, it's safe to assume the interest compounds. If you happen to be using a program like Excel, the interest is compounded in the PV formula. Simple interest is pretty rare.
One area where there is often a mistake is in defining the number of periods and the interest rate. They have to have consistent units, which may require some work. For example, interest is often listed as X% per year. The problem may talk about finding the PV 24 months before the FV, but the number of periods must be in years since the interest rate is listed per year. Therefore, n = 2. As long as the units are consistent, however, finding the PV is done by plug-and-chug.