When calculating a future value (FV), you are calculating how much a given amount of money today will be worth some time in the future. In order to calculate the FV, the other three variables (present value, interest rate, and number of periods) must be known. Recall that the interest rate is represented by either r or i, and the number of periods is represented by either t or n. It is also important to remember that the interest rate and the periods must be in the same units. That is, if the interest rate is 5% per year, one period is one year. However, if the interest rate is 5% per month, t or n must reflect the number of periods in terms of months.
Example 1
What is the FV of a $500, 10-year loan with 7% annual interest?
In this case, the PV is $500, t is 10 years, and i is 7% per year. The next step is to plug these numbers into an equation. But recall that there are two different formulas for the two different types of interest, simple interest and compound interest . If the problem doesn't specify how the interest is accrued, assume it is compound interest, at least for business problems.
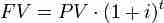
Compound Interest
Interest is paid at the total amount in the account, which may include interest earned in previous periods.
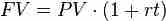
Simple Interest Formula
Simple interest is when interest is only paid on the amount you originally invested (the principal). You don't earn interest on interest you previously earned.
So from the formula, we see that FV=PV(1+i)t so FV=500(1+.07)10. Therefore, FV=$983.58.
In practical terms, you just calculated how much your loan will be in 10 years. This assumes that you don't need to make any payments during the 10 years, and that the interest compounds. Unless the problem states otherwise, it is safe to make these assumptions - you will be told if there are payments during the 10 year period or if it is simple interest.
Example 2
Suppose we want to again find the future value of a $500, 10-year loan, but with an interest rate of 1% per month. In order to get our total number of periods (t), we would multiply 12 months by 10 years, which equals 120 periods. Therefore:
FV=500(1+.01)120
FV=$1,650.19