The future value (FV) measures the nominal future sum of money that a given sum of money is "worth" at a specified time in the future assuming a certain interest rate, or more generally, rate of return. The FV is calculated by multiplying the present value by the accumulation function. The value does not include corrections for inflation or other factors that affect the true value of money in the future. The process of finding the FV is often called capitalization.
On the other hand, the present value (PV) is the value on a given date of a payment or series of payments made at other times. The process of finding the PV from the FV is called discounting.
PV and FV are related , which reflects compounding interest (simple interest has n multiplied by i, instead of as the exponent). Since it's really rare to use simple interest, this formula is the important one.
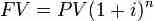
FV of a single payment
The PV and FV are directly related.
PV and FV vary directly: when one increases, the other increases, assuming that the interest rate and number of periods remain constant.
The interest rate (or discount rate) and the number of periods are the two other variables that affect the FV and PV. The higher the interest rate, the lower the PV and the higher the FV. The same relationships apply for the number of periods. The more time that passes, or the more interest accrued per period, the higher the FV will be if the PV is constant, and vice versa.
The formula implicitly assumes that there is only a single payment. If there are multiple payments, the PV is the sum of the present values of each payment and the FV is the sum of the future values of each payment.